Đề Minh Họa Toán Chuyên Lớp 10 Sở GD&ĐT Bà Rịa - Vũng Tàu 2025 - 2026

Đề Minh Họa Tuyển Sinh Lớp 10 Chuyên Toán Sở GD&ĐT Bà Rịa - Vũng Tàu Năm Học 2025 - 2026

Website MeToan.Com trân trọng giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề minh họa kỳ thi tuyển sinh vào lớp 10 THPT chuyên Toán năm học 2025 – 2026 do Sở Giáo dục và Đào tạo tỉnh Bà Rịa – Vũng Tàu công bố.

I. QUY ĐỊNH CHUNG

1. Hình thức thi: Tự luận 100%.
2. Nội dung thi: Theo chương trình GDPT 2018 cấp THCS (chủ yếu lớp 9).
3. Thời gian làm bài thi: 150 phút.
   • Học sinh được sử dụng Máy tính cầm tay không có chức năng soạn thảo văn bản theo quy định của Bộ GD&ĐT.
   • Kiến thức được sử dụng: Như những lưu ý trong kỳ thi Học sinh giỏi lớp 9 cấp tỉnh môn Toán.

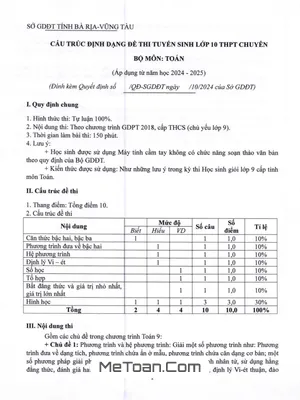
II. CẤU TRÚC ĐỀ THI

1. Thang điểm: Tổng điểm 10.
2. Cấu trúc đề thi. (Thông tin chi tiết về cấu trúc đề thi sẽ được cập nhật sau)

III. NỘI DUNG THI

Đề thi bao gồm các chủ đề trong chương trình Toán 9:

• Chủ đề 1: Phương trình và hệ phương trình:
  • Giải một số phương trình như: Phương trình đưa về dạng tích, phương trình chứa ẩn ở mẫu, phương trình chứa căn dạng cơ bản.
  • Vận dụng một số phương pháp giải phương trình như: đặt ẩn phụ, phân tích thành nhân tử, sử dụng hằng đẳng thức, đánh giá hai vế …
  • Giải một số hệ phương trình cơ bản.
  • Định lý Vi-ét thuận, đảo cho phương trình bậc hai.
  • Điều kiện để phương trình bậc hai có nghiệm, vô nghiệm, có nghiệm kép.
• Chủ đề 2: Bất đẳng thức và bất phương trình:
  • Giải bất phương trình bậc nhất.
  • Hiểu định nghĩa và biết cách chứng minh một số bất đẳng thức cơ bản.
  • Cách tìm giá trị nhỏ nhất và giá trị lớn nhất của một biểu thức.
• Chủ đề 3: Thống kê và xác suất:
  • Nhận dạng và lập bảng, vẽ biểu đồ tần số, tần số tương đối và bảng số liệu ghép nhóm.
  • Mô tả không gian mẫu và tính xác suất của một số biến cố trong trường hợp đơn giản.
• Chủ đề 4: Căn thức bậc hai, bậc ba:
  • Tìm điều kiện và thực hiện được phép tính các biểu thức chứa căn.
• Chủ đề 5: Hình học phẳng:
  • Sử dụng các hệ thức lượng để giải tam giác vuông.
  • Định nghĩa tỉ số lượng giác góc nhọn.
  • Các yếu tố trong đường tròn, tiếp tuyến, các góc trong đường tròn (góc ở tâm, góc nội tiếp).
  • Bài toán liên quan về yếu tố di động hình.
• Chủ đề 6: Số học và tổ hợp:
  • Cách chứng minh chia hết, định nghĩa số nguyên tố.
  • Giải bài toán phương trình trên tập số nguyên.
  • Sử dụng một số nguyên lý như cực hạn, thứ tự, Dirichlet...