Bài Tập Tỷ Số Thể Tích Khối Đa Diện - Lê Bá Bảo
Nâng Cao Kỹ Năng Giải Toán Tỷ Số Thể Tích Khối Đa Diện
Tài liệu "Bài tập tỷ số thể tích khối đa diện" của tác giả Lê Bá Bảo là tài liệu hữu ích dành cho học sinh THPT ôn tập và nâng cao kỹ năng giải toán hình học không gian, đặc biệt là dạng bài tập về tỷ số thể tích khối đa diện.
Với 15 trang, tài liệu cung cấp cho người học:
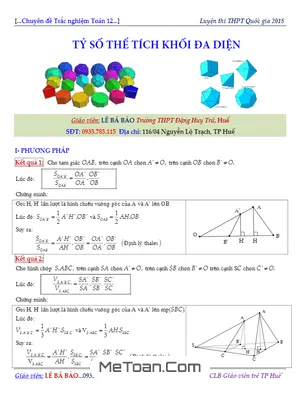
- Phương pháp giải: Trình bày chi tiết các phương pháp giải toán tỷ số thể tích khối đa diện, giúp học sinh nắm vững kiến thức nền tảng.
- Ví dụ mẫu có lời giải: Minh họa phương pháp giải thông qua các ví dụ cụ thể, giúp học sinh dễ dàng tiếp cận và áp dụng vào bài tập thực tế.
- Bài tập rèn luyện: Hệ thống bài tập đa dạng, phong phú, bám sát cấu trúc đề thi, giúp học sinh rèn luyện tư duy và kỹ năng giải toán.
Một số dạng bài tập tiêu biểu trong tài liệu:
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M là trung điểm cạnh SA. Mặt phẳng (α) qua M và song song với (ABCD), cắt các cạnh SB, SC, SD lần lượt tại N, P, Q. Gọi V1 = V(S.ABCD) và V2 = V(S.MNPQ). Khẳng định nào sau đây đúng? A. V1 = 8V2 B. V1 = 6V2 C. V1 = 16V2 D. V1 = 4V2
Cho khối lăng trụ tam giác ABC.A’B’C’, đường thẳng đi qua trọng tâm tam giác ABC song song với BC cắt AB tại D, cắt AC tại E. Mặt phẳng đi qua A, D, E’ chia khối lăng trụ thành hai phần, tỉ số thể tích (số bé chia cho số lớn) của chúng bằng?
Cho tứ diện ABCD. Gọi B’ và C’ lần lượt là trung điểm của AB và AC. Khi đó tỉ số thể tích của khối tứ diện AB’C’D và khối tứ diện ABCD bằng?
Tài liệu "Bài tập tỷ số thể tích khối đa diện - Lê Bá Bảo" là tài liệu tham khảo chất lượng, giúp học sinh tự tin chinh phục dạng toán này trong các kỳ thi quan trọng.























