Đề thi HSG tỉnh Toán 12 năm 2020 - 2021 sở GD&ĐT Bắc Ninh
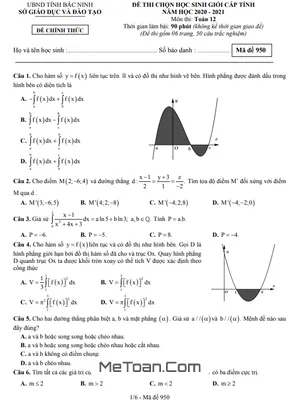
Đề thi HSG Toán 12 năm 2020 - 2021 sở GD&ĐT Bắc Ninh: Lời giải chi tiết và phân tích
MeToan.Com trân trọng giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi chọn học sinh giỏi cấp tỉnh môn Toán lớp 12 năm học 2020 – 2021 sở GD&ĐT Bắc Ninh. Đề thi được biên soạn theo hình thức trắc nghiệm với 50 câu hỏi và bài toán, thời gian làm bài 90 phút, đề thi có đáp án mã đề 543, 511, 009, 950.
Một số nội dung nổi bật trong đề thi:
- Câu hỏi hình học không gian: Đề thi năm nay chú trọng đến các bài toán hình học không gian, yêu cầu thí sinh phải vận dụng linh hoạt các kiến thức về hình học tọa độ, phương pháp tọa độ trong không gian để giải quyết các bài toán tính thể tích, khoảng cách, góc giữa các đường thẳng, mặt phẳng,...
Ví dụ:
Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông ABCD cạnh a, góc giữa mặt bên và mặt phẳng đáy là α thoả mãn cos α = 1/3. Mặt phẳng (P) qua AC và vuông góc với mặt phẳng (SAD) chia khối chóp S.ABCD thành hai khối đa diện. Tỉ lệ thể tích hai khối đa diện là gần nhất với giá trị nào trong các giá trị sau?
- Câu hỏi ứng dụng tích phân: Đề thi cũng có những câu hỏi yêu cầu thí sinh vận dụng kiến thức về tích phân để tính diện tích, thể tích của các vật thể trong không gian.
Ví dụ:
Một khối gỗ hình trụ với bán kính đáy bằng 6 và chiều cao bằng 8. Trên một đường tròn đáy nào đó ta lấy hai điểm A, B sao cho cung AB có số đo 120 độ. Người ta cắt khúc gỗ bởi một mặt phẳng đi qua A, B và tâm của hình trụ (tâm của hình trụ là trung điểm của đoạn nối tâm hai đáy) để được thiết diện như hình vẽ. Biết diện tích S của thiết diện thu được có dạng S = aπ + b√3.Tính P = a + b.
- Câu hỏi về phương trình đường thẳng, mặt phẳng: Các bài toán về viết phương trình đường thẳng, mặt phẳng trong không gian cũng chiếm một phần quan trọng trong đề thi.
Ví dụ:
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (1;1;1), B(2;0;1) và mặt phẳng (P). Viết phương trình chính tắc của đường thẳng d đi qua A, song song với mặt phẳng (P) sao cho khoảng cách từ B đến d lớn nhất.
Kết luận:
Đề thi học sinh giỏi tỉnh Toán 12 năm 2020 – 2021 sở GD&ĐT Bắc Ninh được đánh giá là có tính phân loại cao, bám sát chương trình học và có nhiều câu hỏi hay, sáng tạo, đòi hỏi thí sinh phải có tư duy toán học tốt và khả năng vận dụng kiến thức linh hoạt.























