Đề khảo sát đội tuyển HSG Toán năm 2025 – 2026 trường THPT Đồ Sơn – Hải Phòng
MeToan.Com hân hạnh giới thiệu đến quý thầy, cô giáo và các em học sinh một tài liệu ôn thi cực kỳ giá trị: đề khảo sát đội tuyển học sinh giỏi môn Toán, chuẩn bị cho năm học 2025 – 2026 của trường THPT Đồ Sơn, thành phố Hải Phòng. Đây là một nguồn tài liệu không thể thiếu giúp các em học sinh luyện tập, nâng cao kiến thức và kỹ năng giải Toán chuyên sâu.
Đề thi được biên soạn công phu với cấu trúc đa dạng, nhằm đánh giá toàn diện năng lực của thí sinh trong nhiều mảng kiến thức khác nhau. Cụ thể, đề bao gồm 12 câu trắc nghiệm nhiều phương án lựa chọn, chiếm 3,0 điểm trong tổng số điểm bài thi, đòi hỏi học sinh phải có khả năng phân tích và chọn lọc đáp án chính xác. Tiếp theo là 04 câu trắc nghiệm đúng sai, với tổng 4,0 điểm, yêu cầu sự hiểu biết sâu sắc và khả năng nhận định đúng sai các mệnh đề Toán học. Cuối cùng, 06 câu trắc nghiệm trả lời ngắn, chiếm 3,0 điểm, thử thách khả năng tính toán nhanh và trình bày kết quả ngắn gọn, chính xác của học sinh. Tổng thời gian làm bài là 90 phút, một khoảng thời gian hợp lý để các em thể hiện hết năng lực của mình dưới áp lực thời gian.
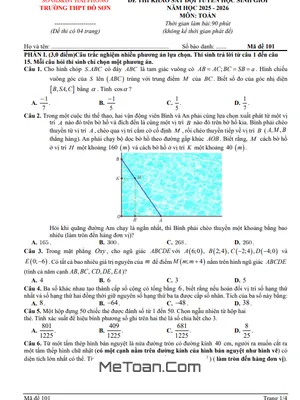
Các bài toán trong đề không chỉ dừng lại ở mức độ vận dụng kiến thức cơ bản mà còn đi sâu vào những vấn đề phức tạp, đòi hỏi tư duy sáng tạo và khả năng giải quyết vấn đề. Chẳng hạn, một trong những câu hỏi nổi bật là bài toán về tối ưu hóa quãng đường di chuyển trong một cuộc thi thể thao, khi hai vận động viên Bình và An phải lựa chọn lộ trình chèo thuyền và chạy bộ sao cho quãng đường của một trong hai người là ngắn nhất. Bài toán này tích hợp kiến thức hình học phẳng, yêu cầu thí sinh xác định vị trí tối ưu và tính toán khoảng cách dựa trên các thông số cho trước về vị trí cắm cờ và bờ hồ. Đây là dạng bài ứng dụng thực tiễn cao, giúp học sinh rèn luyện kỹ năng phân tích tình huống và mô hình hóa bài toán.
Một câu hỏi khác lại đưa học sinh đến với lĩnh vực xác suất và tổ hợp, cụ thể là việc tính xác suất chọn được một tam giác cân nhưng không phải là tam giác đều từ tập hợp các tam giác có các đỉnh là đỉnh của một đa giác đều 18 cạnh nội tiếp đường tròn. Dạng bài này kiểm tra sự nắm vững các nguyên tắc đếm, tính chất của đa giác đều và các loại tam giác đặc biệt, vốn là những kiến thức trọng tâm trong chương trình bồi dưỡng học sinh giỏi Toán.
Không thể thiếu là bài toán về tối ưu thể tích trong hình học không gian. Đề thi có câu hỏi liên quan đến việc cắt ghép một tấm nhôm hình lục giác đều để tạo thành một hình lăng trụ lục giác đều không có nắp. Học sinh được yêu cầu tìm giá trị của biến x (liên quan đến kích thước cắt) sao cho thể tích của khối lăng trụ này đạt giá trị lớn nhất. Đây là một bài toán kinh điển, kết hợp giữa hình học không gian, công thức thể tích và kỹ năng ứng dụng đạo hàm để tìm cực trị, giúp học sinh phát triển khả năng tư duy hàm số và ứng dụng thực tế.
Điểm cộng lớn của đề khảo sát này là việc đi kèm với đáp án chi tiết cho cả hai mã đề 101 và 102. Điều này giúp các em học sinh không chỉ làm bài mà còn có thể tự kiểm tra, đối chiếu kết quả, từ đó rút ra kinh nghiệm và cải thiện những điểm còn yếu. Quý thầy, cô giáo cũng có thể sử dụng bộ đề này như một tư liệu giảng dạy, bồi dưỡng đội tuyển, hoặc làm tài liệu tham khảo để biên soạn các đề kiểm tra chất lượng. MeToan.Com tin rằng đây sẽ là một công cụ hữu ích, đóng góp vào sự thành công của các em học sinh trong hành trình chinh phục kỳ thi Học sinh giỏi Toán sắp tới.























