Phương pháp giải bài toán Đồ thị hàm hợp chứa mũ - lôgarit

Nâng cao kỹ năng giải bài toán Đồ thị hàm hợp chứa mũ - lôgarit trong Toán 12

Tài liệu dài 17 trang này được biên soạn bởi quý thầy, cô giáo Nhóm Toán VDC & HSG THPT, là cẩm nang hữu ích giúp học sinh lớp 12 nắm vững phương pháp giải bài toán Đồ thị hàm hợp chứa mũ - lôgarit, một dạng toán thường gặp trong chương trình Giải tích lớp 12, chương 2.

Tài liệu đi sâu vào phân tích và hướng dẫn giải các bài toán ví dụ điển hình, giúp học sinh rèn luyện tư duy và kỹ năng giải toán hiệu quả. Dưới đây là một số dạng bài toán được trình bày trong tài liệu:

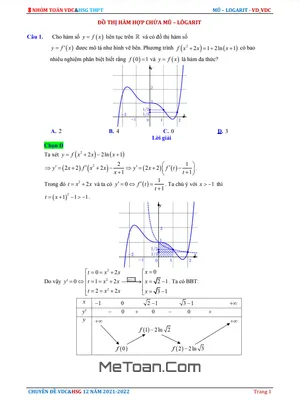
• Bài toán 1: Cho hàm số y = f(x) liên tục trên R và có đồ thị hàm số y = f(x) được mô tả như hình vẽ. Phương trình 2f(xx) + x2 - 1 = 2ln|x - 1| có bao nhiêu nghiệm phân biệt biết rằng f(0) = 1 và y = f(x) là hàm đa thức?
• Bài toán 2: Cho hàm số bậc bốn f(x) có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của m thuộc [-2021; 2021] để phương trình sau có hai nghiệm dương phân biệt?
• Bài toán 3: Cho hàm số y = f(x) là hàm số chẵn trên tập số thực và có đồ thị như hình vẽ. Biết rằng tồn tại các giá trị của tham số m để phương trình f(x2 - 3) + 2f(x3 - 3m) - 4f(x3) + 3m = 0 có đúng 7 nghiệm thực phân biệt. Tổng lập phương các giá trị đó của m là?
• Bài toán 4: Cho hàm số y = f(x) có đạo hàm trên R và có bảng biến thiên sau: Có bao nhiêu giá trị nguyên của m để phương trình ... có đúng 2 nghiệm phân biệt?
• Bài toán 5: Cho hàm số y = f(x) có đồ thị như hình vẽ. Biết f(3) = 10. Có bao nhiêu giá trị nguyên của m để phương trình 2x.f(f(f(x))) = em có bốn nghiệm..

Với việc phân tích chi tiết các dạng bài tập và cung cấp lời giải cụ thể, tài liệu này sẽ là nguồn tài liệu tham khảo vô cùng hữu ích cho các em học sinh lớp 12 trong quá trình ôn tập và nâng cao kỹ năng giải toán Đồ thị hàm hợp chứa mũ - lôgarit.