Phân Dạng Và Kỹ Thuật Giải Toán Hàm Số Và Đồ Thị - Trần Thanh Hiền

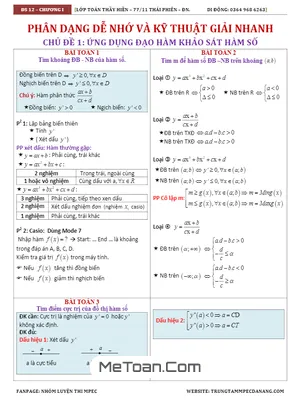
MeToan.Com giới thiệu đến các em tài liệu phân dạng dễ nhớ và kỹ thuật giải nhanh bài toán ứng dụng đạo hàm để khảo sát hàm số do thầy Trần Thanh Hiền biên soạn. Tài liệu gồm 23 trang với nội dung gồm 2 phần:

Phần 1: Tóm tắt phương pháp giải nhanh 14 dạng toán thường gặp trong chủ đề ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số.

Phần 2: 125 bài toán trắc nghiệm hàm số và đồ thị có đáp án. Các bài toán được sắp xếp thành các dạng bài:

CHUYÊN ĐỀ 1: TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ

• BÀI TOÁN 1. TÌM KHOẢNG ĐỒNG BIẾN – NGHỊCH BIẾN.
  • Dạng 1. Hàm bậc 3.
  • Dạng 2. Hàm bậc 4.
  • Dạng 3. Hàm phân thức.
  • Dạng 4. Hàm số khác.
  • Dạng 5. Dựa vào đồ thị và bảng biến thiên.
• BÀI TOÁN 2. TÌM M ĐỂ HÀM SỐ ĐỒNG BIẾN – NGHỊCH BIẾN TRÊN (A; B).
  • Dạng 1. Hàm bậc ba đồng biến – nghịch biến trên R.
  • Dạng 2. Hàm phân thức đồng biến – nghịch biến trên tập xác định.
  • Dạng 3. Hàm đa thức đồng biến – nghịch biến trên (a;b).
  • Dạng 4. Hàm phân thức đồng biến – nghịch biến trên (a;b).

CHUYÊN ĐỀ 2. CỰC TRỊ

• BÀI TOÁN 3. TÌM CỰC TRỊ CỦA HÀM SỐ.
  • Dạng 1. Tìm điểm cực trị.
• BÀI TOÁN 4. BÀI TOÁN CỰC TRỊ CHỨA THAM SỐ M.
  • Dạng 2. Đường thẳng qua hai điểm cực trị.
  • Dạng 3. Tìm m biết hàm số có 1 cực trị cho trước.
  • Dạng 4. Tìm m để hàm bậc ba không có hoặc 2 cực trị.
  • Dạng 5. Tìm m để hàm trùng phương có 1 hoặc 3 cực trị.
  • Dạng 6. Tìm m để hàm bậc ba có 2 cực trị thỏa điều kiện cho trước.
  • Dạng 7. Tìm m để hàm trùng phương có 3 cực trị thỏa điều kiện cho trước.
  • Dạng 8. Tính chất cực trị hàm số.
  • Dạng 9. Tìm số cực trị của hàm số.

CHUYÊN ĐỀ 3. GIÁ TRỊ LỚN NHẤT – NHỎ NHẤT CỦA HÀM SỐ

• BÀI TOÁN 5. TÌM GIÁ TRỊ LỚN NHẤT – NHỎ NHẤT.
  • Dạng 1. Tìm GTLN – GTNN.
• BÀI TOÁN 6. BÀI TOÁN GTLN – GTNN CHỨA THAM SỐ M.
  • Dạng 2. Tìm m để hàm số có GTLN – GTNN.
  • Dạng 3. Bài toán thực tế.

CHUYÊN ĐỀ 4. ĐƯỜNG TIỆM CẬN

• BÀI TOÁN 7. TÌM ĐƯỜNG TIỆM CẬN.
  • Dạng 1. Tìm đường tiệm cận.
  • Dạng 2. Dựa vào bảng biến thiên tìm tiệm cận.
• BÀI TOÁN 8. BÀI TOÁN TIỆM CẬN CÓ CHỨA THAM SỐ M.
  • Dạng 3. Tìm m để hàm số có tiệm cận đứng.
  • Dạng 4. Tìm m để hàm số có tiệm cận ngang.

CHUYÊN ĐỀ 5. ĐỒ THỊ HÀM SỐ

• BÀI TOÁN 9. NHẬN DẠNG ĐỒ THỊ.
  • Dạng 1. Nhận dạng đồ thị hàm bậc ba.
  • Dạng 2. Nhận dạng đồ thị hàm trùng phương.
  • Dạng 3. Nhận dạng đồ thị hàm phân thức.
  • Dạng 4. Nhận dạng đồ thị hàm trị tuyệt đối.
• BÀI TOÁN 10. BÀI TOÁN 10 HÀM ẨN F'(X).

CHUYÊN ĐỀ 6. SỰ TƯƠNG GIAO CỦA HAI ĐỒ THỊ

• BÀI TOÁN 11. TỌA ĐỘ GIAO ĐIỂM.
  • Dạng 1. Tìm tọa độ giao điểm.
• BÀI TOÁN 12. BÀI TOÁN TƯƠNG GIAO CÓ CHỨA THAM SỐ M.
  • Dạng 2. Biện luận số giao điểm của hai đồ thị.
  • Dạng 3. Tìm m để hàm số có số giao điểm cho trước.
  • Dạng 4. Tìm số giao điểm của hàm trị tuyệt đối.
  • Dạng 5. Tìm số giao điểm của hàm ẩn.
  • Dạng 6. Tìm số giao điểm dựa vào bảng biến thiên.

CHUYÊN ĐỀ 7. ĐƯỜNG TIẾP TUYẾN

• BÀI TOÁN 13. VIẾT PHƯƠNG TRÌNH TIẾP TUYẾN.
  • Dạng 1. Viết phương trình tiếp tuyến.
• BÀI TOÁN 14. BÀI TOÁN TIẾP TUYẾN CHỨA THAM SỐ M.
  • Dạng 2. Tìm m đồ thị có tiếp tuyến thỏa đk cho trước.
  • Dạng 3. Điều kiện tiếp xúc.