Đề KSCL giữa HK2 Toán 9 năm 2018 - 2019 phòng GD&ĐT Bắc Từ Liêm - Hà Nội

Đề Kiểm Tra Giữa Kì 2 Môn Toán Lớp 9 Năm 2018 - 2019 Phòng GD&ĐT Bắc Từ Liêm - Hà Nội
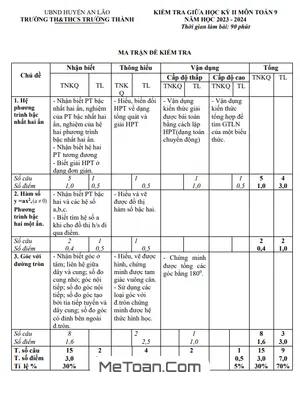
Đề kiểm tra giữa học kỳ 2 môn Toán lớp 9 năm học 2018 - 2019 của phòng GD&ĐT Bắc Từ Liêm - Hà Nội được biên soạn nhằm mục đích giúp học sinh ôn tập và củng cố kiến thức đã học từ đầu học kỳ 2. Đề thi được ra dưới hình thức tự luận gồm 05 bài toán, thời gian làm bài 120 phút. Cấu trúc đề thi bám sát chương trình học và có nhiều nét tương đồng với đề thi tuyển sinh vào lớp 10 môn Toán.
Dưới đây là một số nội dung tiêu biểu trong đề KSCL giữa HK2 Toán 9 năm 2018 - 2019 phòng GD&ĐT Bắc Từ Liêm - Hà Nội:
Bài toán thực tế: Yêu cầu học sinh giải bài toán bằng cách lập phương trình hoặc hệ phương trình. Ví dụ: Bài toán về mua bán với giá niêm yết và khuyến mãi.
Hình học: Đề thi bao gồm các bài toán liên quan đến đường tròn, tam giác, tứ giác nội tiếp, chứng minh hình học, góc, tỷ số đồng dạng....
Ví dụ minh họa:
Bài toán giải bằng cách lập phương trình hoặc hệ phương trình: Một người mua một cái bàn là và một cái quạt điện với tổng số tiền theo giá niêm yết là 750 nghìn đồng. Khi trả tiền người đó được khuyến mãi giảm 10% đối với giá tiền bàn là và 20% đối với giá tiền quạt điện so với giá niêm yết. Vì vậy, người đó phải trả tổng cộng 625 nghìn đồng. Tính giá tiền của cái bàn là và cái quạt điện theo giá niêm yết?
Bài toán hình học: Cho (O;R) đường kính AB cố định, điểm H nằm giữa hai điểm A và O. Kẻ dây CD vuông góc với AB tại H. Lấy điểm F thuộc cung AC nhỏ; BF cắt CD tại E; AF cắt tia DC tại I.
- Chứng minh: Tứ giác AHEF là tứ giác nội tiếp.
- Chứng minh: góc BFH = EAB, từ đó suy ra BE.BF = BH.BA.
- Đường tròn ngoại tiếp tam giác IEF cắt AB tại điểm thứ hai M. Chứng minh: tam giác HBE đồng dạng với tam giác HIA và điểm M thuộc (O;R).
- Tìm vị trí của H trên OA để tam giác OHD có chu vi lớn nhất.