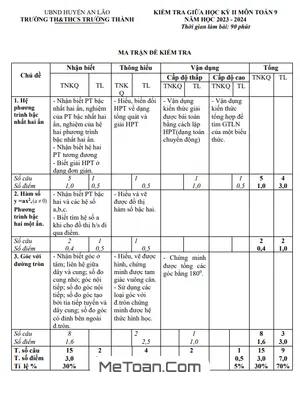
Đề giữa kì 2 Toán 9 năm 2024 – 2025 trường THCS Đinh Tiên Hoàng – Khánh Hòa
MeToan.Com hân hạnh giới thiệu đến quý thầy, cô giáo và các em học sinh bộ đề kiểm tra giữa học kì 2 môn Toán lớp 9, được biên soạn đặc biệt dành cho năm học 2024 – 2025 của trường THCS Đinh Tiên Hoàng, thị xã Ninh Hòa, tỉnh Khánh Hòa. Đây là một tài liệu ôn tập vô cùng quý giá, không chỉ giúp các em học sinh đánh giá lại kiến thức đã học mà còn đi kèm với đáp án chi tiết, lời giải cụ thể và hướng dẫn chấm điểm rõ ràng, tạo điều kiện thuận lợi nhất cho việc tự học và chuẩn bị kĩ càng cho kì thi quan trọng sắp tới.
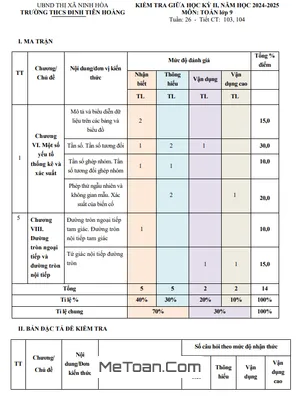
Cấu trúc đề thi được xây dựng một cách khoa học, bám sát ma trận kiến thức trọng tâm của chương trình Toán lớp 9 học kì 2, bao gồm các nội dung cốt lõi từ hai chương chính: "Một số yếu tố thống kê và xác suất" cùng với "Đường tròn ngoại tiếp và đường tròn nội tiếp".
Chương VI: Một số yếu tố thống kê và xác suất
- Mô tả và biểu diễn dữ liệu trên các bảng và biểu đồ: Phần này tập trung vào khả năng của học sinh trong việc thu thập, sắp xếp, tổ chức và trình bày dữ liệu một cách trực quan. Các em sẽ cần thành thạo trong việc lập bảng tần số, bảng tần số tương đối, cũng như vẽ các loại biểu đồ phổ biến như biểu đồ cột, biểu đồ tròn, biểu đồ đoạn thẳng để mô tả các tập dữ liệu khác nhau. Việc hiểu rõ cách chọn loại biểu đồ phù hợp với từng dạng dữ liệu là một kĩ năng quan trọng.
- Tần số. Tần số tương đối: Nội dung này yêu cầu học sinh nắm vững định nghĩa, cách tính toán và ý nghĩa của tần số (số lần xuất hiện của một giá trị trong tập dữ liệu) và tần số tương đối (tỉ lệ phần trăm của tần số so với tổng số giá trị). Đây là những khái niệm cơ bản để phân tích và hiểu dữ liệu thống kê.
- Tần số ghép nhóm. Tần số tương đối ghép nhóm: Khi làm việc với các tập dữ liệu lớn hoặc dữ liệu liên tục, việc nhóm dữ liệu thành các khoảng (lớp) là cần thiết. Học sinh sẽ được kiểm tra về khả năng xây dựng bảng tần số ghép nhóm, tính toán tần số tương đối ghép nhóm và diễn giải thông tin từ các bảng này một cách chính xác.
- Phép thử ngẫu nhiên và không gian mẫu. Xác suất của biến cố: Đây là phần mở đầu về xác suất. Các em cần hiểu thế nào là phép thử ngẫu nhiên, cách xác định không gian mẫu (tập hợp tất cả các kết quả có thể xảy ra của một phép thử) và các biến cố (tập con của không gian mẫu). Trọng tâm là biết cách tính xác suất của một biến cố đơn giản dựa trên công thức cơ bản: số kết quả thuận lợi chia cho tổng số kết quả có thể xảy ra.
Chương VIII: Đường tròn ngoại tiếp và đường tròn nội tiếp
- Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác: Phần này đi sâu vào các khái niệm về đường tròn ngoại tiếp (đi qua ba đỉnh của tam giác) và đường tròn nội tiếp (tiếp xúc với ba cạnh của tam giác). Học sinh cần nắm vững cách xác định tâm và bán kính của các đường tròn này (tâm đường tròn ngoại tiếp là giao điểm ba đường trung trực, tâm đường tròn nội tiếp là giao điểm ba đường phân giác), cũng như các tính chất liên quan.
- Tứ giác nội tiếp đường tròn: Đây là một chủ đề quan trọng trong hình học phẳng. Học sinh sẽ được kiểm tra về định nghĩa tứ giác nội tiếp (tứ giác có bốn đỉnh nằm trên một đường tròn), các dấu hiệu nhận biết một tứ giác nội tiếp (ví dụ: tổng hai góc đối bằng 180 độ; hai đỉnh kề cùng nhìn một cạnh dưới một góc bằng nhau) và các tính chất đặc trưng của chúng. Việc vận dụng các tính chất này để giải các bài toán hình học là mục tiêu chính của phần này.
Thông qua việc ôn luyện kĩ lưỡng với đề thi này, học sinh không chỉ củng cố kiến thức mà còn rèn luyện kĩ năng giải đề, giúp các em tự tin hơn khi bước vào kì thi chính thức.