Cực Trị Của Hàm Số - Lê Văn Đoàn
Cực Trị Của Hàm Số - Tài Liệu Ôn Tập Hiệu Quả Giải Tích 12
Tài liệu 58 trang được biên soạn bởi thầy Lê Văn Đoàn, cung cấp một cái nhìn tổng quan về cực trị của hàm số, bao gồm lý thuyết, phân dạng bài tập, hướng dẫn giải chi tiết và bài tập trắc nghiệm/ tự luận. Tài liệu hỗ trợ học sinh lớp 12 tự học chương 1 Giải tích 12: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số.
Nội Dung Chính:
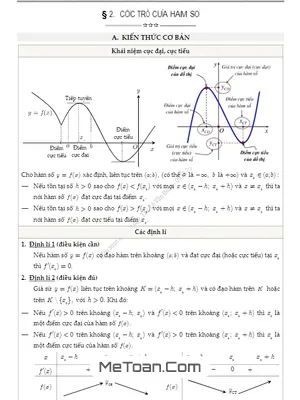
A. KIẾN THỨC CƠ BẢN
Phần này giúp học sinh ôn tập lại những kiến thức nền quan trọng về cực trị của hàm số, bao gồm định nghĩa, điều kiện tồn tại cực trị, ...
B. CÁC DẠNG TOÁN THƯỜNG GẶP VÀ PHƯƠNG PHÁP GIẢI
Phần này là trọng tâm của tài liệu, tập trung vào các dạng toán thường gặp trong các kỳ thi và phương pháp giải chi tiết cho từng dạng:
Dạng toán 1: Tìm điểm cực đại, cực tiểu, giá trị cực đại, giá trị cực tiểu.
- Bài toán: Tìm các điểm cực đại, cực tiểu (nếu có) của hàm số y = f(x).
- Phương pháp: Gồm 4 bước chi tiết từ việc tìm tập xác định, tính đạo hàm, lập bảng biến thiên đến kết luận cực trị dựa trên định lý.
Dạng toán 2: Tìm tham số m để hàm số đạt cực trị tại điểm x = xo cho trước. Phương trình đường thẳng nối hai điểm cực trị.
- Bài toán: Tìm tham số để hàm số y = f(x) đạt cực trị tại điểm x = x0?
- Phương pháp: Áp dụng định lý về điều kiện để hàm số đạt cực trị tại một điểm, kết hợp giải phương trình và thử lại.
- Lưu ý: Phân biệt cách thử lại với hàm bậc ba và các hàm số khác.
Dạng toán 3: Biện luận hoành độ cực trị (Vận dụng & vận dụng cao).
Phần này nâng cao, giúp học sinh giải quyết các bài toán biện luận số lượng điểm cực trị của hàm số dựa vào tham số.
Dạng toán 4: Cực trị của hàm hợp và hàm số trị tuyệt đối (vận dụng cao).
Phần này trang bị kiến thức về cực trị cho hàm hợp và hàm trị tuyệt đối, thường xuất hiện trong các câu hỏi vận dụng cao.
Tài liệu của thầy Lê Văn Đoàn là một tài liệu hữu ích, giúp học sinh nắm vững kiến thức về cực trị của hàm số, từ đó tự tin chinh phục các kỳ thi.























