Chuyên Đề Hàm Số Lượng Giác Và Phương Trình Lượng Giác - Võ Anh Dũng
Tài liệu này cung cấp cho bạn đọc kiến thức trọng tâm và phương pháp giải các dạng bài tập thường gặp về hàm số lượng giác và phương trình lượng giác trong chương trình Toán học lớp 11.
Nội dung tài liệu được chia thành ba phần chính:
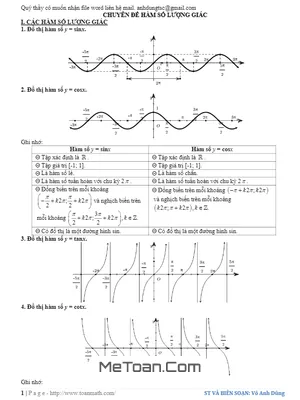
I. Các Hàm Số Lượng Giác
Phần này tập trung vào các dạng bài tập phổ biến liên quan đến hàm số lượng giác, bao gồm:
- Dạng 1: Tìm tập xác định của hàm số lượng giác.
- Dạng 2: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số lượng giác.
- Dạng 3: Tìm chu kỳ của hàm số lượng giác.
- Dạng 4: Xét tính đồng biến, nghịch biến của hàm số lượng giác.
Mỗi dạng bài tập đều được trình bày chi tiết về phương pháp giải, kèm theo ví dụ minh họa giúp người học dễ dàng nắm bắt và áp dụng.
II. Phương Trình Lượng Giác
Phần này đi sâu vào các loại phương trình lượng giác thường gặp trong chương trình học, bao gồm:
- Phương trình lượng giác cơ bản: Ôn tập các công thức lượng giác cơ bản và phương pháp giải các phương trình lượng giác đơn giản.
- Phương trình bậc hai đối với một hàm số lượng giác: Hướng dẫn cách giải phương trình bậc hai chứa hàm số lượng giác bằng cách đặt ẩn phụ.
- Phương trình bậc nhất đối với sinx và cosx: Giới thiệu phương pháp giải phương trình bậc nhất chứa đồng thời sinx và cosx.
- Phương trình đẳng cấp bậc hai: Trình bày cách nhận biết và phương pháp giải phương trình đẳng cấp bậc hai đối với hàm số lượng giác.
- Phương trình đối xứng: Hướng dẫn cách giải các dạng phương trình đối xứng đối với hàm số lượng giác.
III. Bài Tập Trắc Nghiệm
Phần này cung cấp cho người học một bộ bài tập trắc nghiệm đa dạng, bám sát nội dung đã học ở hai phần trên. Qua đó, giúp học sinh củng cố kiến thức, rèn luyện kỹ năng giải bài tập và làm quen với dạng bài thi trắc nghiệm.
Với nội dung được trình bày cô đọng, dễ hiểu cùng hệ thống bài tập phong phú, tài liệu “Chuyên Đề Hàm Số Lượng Giác Và Phương Trình Lượng Giác - Võ Anh Dũng” là tài liệu hữu ích cho học sinh lớp 11 trong quá trình học tập và ôn luyện môn Toán, đặc biệt là để chinh phục các kỳ thi quan trọng.