Chuyên Đề Cực Trị Của Hàm Số - Hoàng Xuân Nhàn

Tài liệu gồm 62 trang, được biên soạn bởi thầy giáo Hoàng Xuân Nhàn, tổng hợp lý thuyết SGK, phân dạng, hướng dẫn giải, ví dụ minh họa và bài tập rèn luyện chuyên đề cực trị của hàm số, giúp học sinh học tốt chương trình Giải tích 12 chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số.

A. LÝ THUYẾT SGK CẦN GHI NHỚ

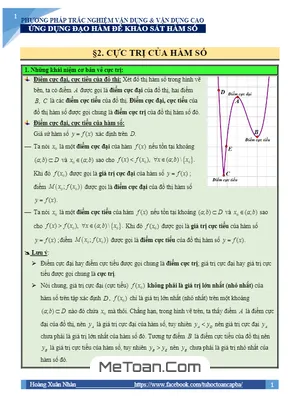
1. Những khái niệm cơ bản về cực trị của hàm số.
2. Điều kiện có cực trị của hàm số.

B. CÁC DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI TOÁN

Dạng toán 1. Xét dấu đạo hàm để tìm cực trị của hàm số.

• Bài toán 1: Tính đạo hàm để tìm cực trị của hàm số y = f(x).
• Bài toán 2: Tìm cực trị của hàm số dựa vào bảng biến thiên hoặc đạo hàm (cho sẵn).

Dạng toán 2. Tìm tham số thỏa mãn điều kiện cực trị của hàm số.

• Bài toán 1: Tìm tham số thỏa mãn điều kiện cực trị của hàm số y = ax^3 + bx^2 + cx + d.
• Bài toán 2: Bài toán tham số có liên quan đến đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y = ax^3 + bx^2 + cx + d.
• Bài toán 3: Bài toán tìm tham số thỏa mãn điều kiện cực trị hàm số y = ax^4 + bx^2 + c.
• Bài toán 4: Tìm tham số thỏa mãn điều kiện cực trị của những hàm số khác.

C. BÀI TẬP RÈN LUYỆN

Tuyển chọn 100 bài tập trắc nghiệm cực trị của hàm số có đáp án.

Xem thêm: Chuyên Đề Tính Đơn Điệu Của Hàm Số - Hoàng Xuân Nhàn.