Bài Tập Trắc Nghiệm Hàm Số Lượng Giác Và Phương Trình Lượng Giác - Phan Hữu Thế

Kiến Thức Cần Nắm Vững Để Giải Bài Tập Trắc Nghiệm Hàm Số Lượng Giác Và Phương Trình Lượng Giác
Để tự tin chinh phục các bài tập trắc nghiệm liên quan đến hàm số lượng giác và phương trình lượng giác, bạn cần nắm vững những kiến thức nền tảng sau đây:
Giá trị lượng giác của các góc có liên quan đặc biệt:
- Nắm rõ các giá trị sin, cos, tan, cot của các góc đặc biệt (0°, 30°, 45°, 60°, 90°, ...) và các góc có liên quan đến chúng (góc bù, phụ, đối, ...).
Phương trình lượng giác cơ bản:
- Phương trình sinx = sina
- Phương trình cosx = cosa
- Phương trình tanx = tana
- Phương trình cotx = cota
- Hiểu rõ cách giải tổng quát và cách tìm nghiệm trong các trường hợp cụ thể.
Một số lưu ý quan trọng:
- Điều kiện xác định của phương trình lượng giác.
- Cách biến đổi phương trình lượng giác bằng cách sử dụng các công thức lượng giác.
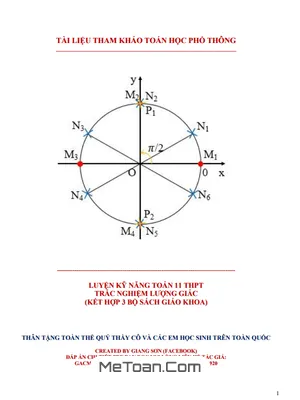
- Cách biểu diễn nghiệm của phương trình lượng giác trên đường tròn lượng giác.
Các Dạng Phương Trình Lượng Giác Thường Gặp
Ngoài những kiến thức cơ bản, bạn cần làm quen với các dạng phương trình lượng giác thường gặp sau:
Phương trình bậc nhất đối với một hàm số lượng giác:
- Ví dụ: sinx = a, cos2x = b, ...
Phương trình bậc hai đối với một hàm số lượng giác:
- Ví dụ: sin²x + 2sinx - 1 = 0, ...
Phương trình bậc nhất đối với sinx và cosx:
- Ví dụ: asinx + bcosx = c
Phương trình bậc nhất theo sinx và cosx dạng mở rộng:
- Dạng 1: asinx + bcosx = √(a² + b²)sinkx
- Dạng 2: asinkx + bcoskx = bsinqx + acosqx
- Dạng 3: Phương trình đẳng cấp: asin²x + bsinxcosx + ccos²x = 0
- Dạng 4: Phương trình đối xứng và phản đối xứng: a(sinx + cosx) + bsinxcosx + c = 0
Bằng việc nắm vững kiến thức nền tảng và luyện tập thường xuyên với các dạng bài tập, bạn sẽ tự tin chinh phục các bài tập trắc nghiệm hàm số lượng giác và phương trình lượng giác trong các kỳ thi quan trọng.