50 Bài Tập Trắc Nghiệm Tính Đơn Điệu Của Hàm Hợp Có Đáp Án Và Lời Giải

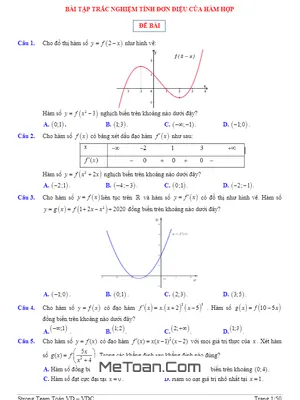
Tài liệu gồm 53 trang, được biên soạn bởi quý thầy, cô giáo nhóm Strong Team Toán VD – VDC, tuyển tập 50 bài tập trắc nghiệm tính đơn điệu của hàm hợp có đáp án và lời giải chi tiết. Giúp học sinh ôn tập, củng cố kiến thức và rèn luyện kỹ năng giải bài tập về tính đơn điệu của hàm hợp.

Trích dẫn tài liệu

Dưới đây là một số ví dụ về các bài tập trong tài liệu:

Bài tập 1:

Cho hàm số y = f(x) có đạo hàm f'(x) = x(x – 1)^2.(x – 2) với mọi giá trị thực của x. Xét hàm số g(x) = f(5x/(x^2 + 4)). Trong các khẳng định sau khẳng định nào đúng? A. Hàm số đồng biến trên khoảng (0;1). B. Hàm số nghịch biến trên khoảng (0;4). C. Hàm số đạt cực đại tại x = 0. D. Hàm số đạt giá trị nhỏ nhất tại x = 1.

Bài tập 2:

Cho hàm số y = f(x) xác định trên R và có bảng xét dấu đạo hàm như sau. Biết f(x) > 2 với mọi x thuộc R. Xét hàm số g(x) = f(3 – 2f(x)) – x^3 + 3x^2 – 2020. Khẳng định nào sau đây đúng? A. Hàm số g(x) đồng biến trên khoảng (-2;-1). B. Hàm số g(x) nghịch biến trên khoảng (0;1). C. Hàm số g(x) đồng biến trên khoảng (3;4). D. Hàm số g(x) nghịch biến trên khoảng (2;3).

Bài tập 3:

Cho hàm số y = f(x) xác định trên R. Hàm số y = g(x) = f'(2x + 3) + 2 có đồ thị là một parabol với tọa độ đỉnh I(2;-1) và đi qua điểm A (1;2). Hỏi hàm số y = f(x) nghịch biến trên khoảng nào dưới đây?

Xem thêm: 138 bài toán chọn lọc tính đơn điệu của hàm hợp – Nguyễn Hoàng Việt.