Đề thi thử tốt nghiệp THPT 2024 lần 1 môn Toán sở GD&ĐT Lạng Sơn

MeToan.Com giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi thử tốt nghiệp THPT năm 2024 lần 1 môn Toán sở Giáo dục và Đào tạo tỉnh Lạng Sơn; kỳ thi được diễn ra vào thứ Ba ngày 27 tháng 02 năm 2024; đề thi có đáp án trắc nghiệm mã đề 101 102 103 104 105 106 107 108 và lời giải chi tiết các bài toán vận dụng – vận dụng cao.

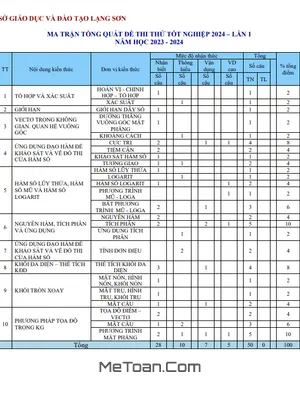
Ma trận Đề thi thử tốt nghiệp THPT năm 2024 lần 1 môn Toán sở GD&ĐT Lạng Sơn:

Bài toán chỉ sử dụng tổ hợp.
Xác suất của bài toán chọn nhóm.
Giới hạn phân thức có bậc tử bằng bậc mẫu.
Góc giữa cạnh bên với mặt đáy.
Khoảng cách từ chân đường cao đến mặt xiên trong hình chóp.
Tìm cực trị của hàm số khi biết đồ thị hàm số.
Tìm cực trị của hàm số khi biết bảng biến thiên.
Tìm m để hàm số đạt cực trị tại 1 điểm x0 cho trước.
Tìm số điểm cực trị của hàm số |f(u)| khi biết đồ thị, bảng biến thiên f’(x).
Tìm tiệm cận f(x) dựa vào bảng biến thiên f(x).
Tìm đường tiệm cận, số đường tiệm cận của hàm số.
Nhận dạng bảng biến thiên hàm số bậc 3.
Tìm tọa độ giao điểm của đồ thị hai hàm số khi biết f(x) và g(x).
Tìm số nghiệm của phương trình f(x) = a khi biết đồ thị, bảng biến thiên f(x).
Tập xác định của hàm số lũy thừa có số mũ hữu tỷ.
Dùng công thức biến đổi cơ số logarit rút gọn biểu thức.
Tính đạo hàm của hàm số logarit.
Tìm Min, Max của biểu thức khi có điều kiện f(u) = f(v) chứa logarit.
Tìm số giá trị nguyên của y để phương trình Loga có nghiệm thỏa mãn điều kiện bằng phương pháp đánh giá.
Bất phương trình mũ cơ bản.
Bất phương trình logarit cơ bản.
Bất phương trình logarit dạng tích.
Nguyên hàm cơ bản của hàm số đa thức.
Nguyên hàm cơ bản của hàm lượng giác.
Định nghĩa của tích phân.
Tính chất của tích phân.
Tích phân của hàm ẩn bằng phương pháp từng phần.
Tích phân của hàm ẩn bằng tạo ra công thức đạo hàm tích, thương.
Biết f’(x), tính tích phân f(x).
Ý nghĩa hình học của tích phân.
Tìm khoảng đơn điệu của hàm số khi biết f’(x), bảng xét dấu f’(x).
Xét tính đơn điệu của hàm số f(x) khi biết đồ thị, bảng biến thiên f’(x).
Áp dụng công thức tính thể tích khối chóp.
Áp dụng công thức tính thể tích khối lăng trụ.
Tính chiều cao, khoảng cách bằng thể tích.
Thể tích khối lăng trụ đứng có góc giữa hai mặt phẳng.
Tính V, Sxq hoặc Stp khi biết R, h, l.
Tính Sxq hoặc Stp khi biết R và h.
Tính V, S khi biết R.
Bài toán kết hợp hình cầu với hình trụ.
Xác định tọa độ vectơ qua phép cộng, trừ vectơ.
Tính độ dài đoạn thẳng khi biết hai đầu mút, độ dài vectơ.
Xác định tọa độ tâm, R, S, V của mặt cầu khi biết phương trình mặt cầu.
Viết phương trình mặt cầu khi biết tâm và đi qua 1 điểm.
Nhận diện phương trình mặt cầu.
Xác định VTPT khi biết phương trình mặt phẳng.
Nhận diện điểm thuộc mặt phẳng.
Viết phương trình mặt phẳng trung trực của đoạn thẳng.
Tính khoảng cách từ điểm đến mặt phẳng.
Viết phương trình mặt phẳng chắn hai đoạn theo tỉ số.