Đề thi thử Toán THPT Quốc gia 2020 lần 1 trường THPT Trần Phú – Hà Tĩnh

Trường THPT Trần Phú tổ chức kỳ thi thử tốt nghiệp THPT Quốc gia môn Toán lần 1 năm học 2019 - 2020

Vào chiều thứ Bảy, ngày 11 tháng 01 năm 2020, trường THPT Trần Phú, tỉnh Hà Tĩnh đã tổ chức kỳ thi thử THPT Quốc gia môn Toán lần thứ nhất cho học sinh khối 12, năm học 2019 – 2020.

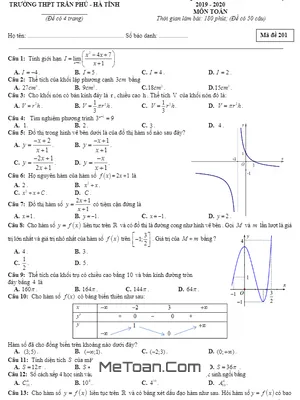
Đề thi thử Toán THPT Quốc gia 2020 lần 1 trường THPT Trần Phú – Hà Tĩnh mã đề 201 gồm 04 trang với 50 câu trắc nghiệm, thời gian làm bài 90 phút.

Một số nội dung đáng chú ý trong đề thi thử Toán lần 1 trường THPT Trần Phú – Hà Tĩnh

Dưới đây là một số câu hỏi trích dẫn từ đề thi thử Toán THPT Quốc gia 2020 lần 1 trường THPT Trần Phú – Hà Tĩnh:

Trong không gian cho hai điểm A, B cố định và độ dài đoạn thẳng AB bằng 4. Biết rằng tập hợp các điểm M sao cho MA = 3MB là một mặt cầu. Tìm bán kính R của mặt cầu đó?
Hãng pha lê nổi tiếng Swarovski của Áo dự định thiết kế một viên pha lê hình cầu và đặt vào bên trong nó 7 viên ruby hình cầu nhỏ hơn, trong đó viên ruby ở chính giữa có tâm trùng với tâm của viên pha lê và tiếp xúc với 6 viên ruby còn lại, 6 viên ruby còn lại có kích thước bằng nhau và nằm ở các vị trí đối xứng nhau (qua tâm của viên pha lê) và tiếp xúc với viên pha lê (như hình vẽ). Biết viên pha lê có đường kính 10 cm và hãng này muốn thiết kế sao cho tổng thể tích các viên ruby bên trong là nhỏ nhất để tiết kiệm được lượng ruby. Khi đó bán kính của viên ruby ở giữa mà hãng pha lê cần thiết kế gần giá trị nào nhất sau đây?
Một người gửi 150 triệu đồng vào ngân hàng với kì hạn 3 tháng (một quý), lãi suất 5% một quý theo hình thức lãi kép. Sau đúng 6 tháng người đó gửi thêm 150 triệu đồng với hình thức và lãi suất như trên. Hỏi sau đúng một năm tính từ lần gửi đầu tiên người đó nhận được số tiền gần với kết quả nào nhất?
Cho khối chóp S.ABCD có thể tích bằng 1 và đáy ABCD là hình bình hành. Trên cạnh SC lấy điểm E sao cho SE = 2EC. Tính thể tích V của khối tứ diện SEBD.
Gieo đồng thời hai con súc sắc cân đối và đồng chất. Tính xác suất P để hiệu số chấm trên các mặt xuất hiện của hai con súc sắc bằng 2.