Ôn Tập Giữa Kì 2 Toán 11 Năm 2022 - 2023 Trường THPT Trần Phú - Hà Nội

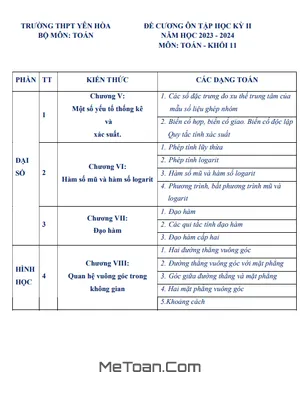
Đề Cương Ôn Tập Giữa Kì 2 Môn Toán 11 - Trường THPT Trần Phú - Hà Nội
Website MeToan.Com xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 11 đề cương ôn tập kiểm tra giữa học kì 2 môn Toán 11 năm học 2022 – 2023 của trường THPT Trần Phú, quận Hoàn Kiếm, thành phố Hà Nội.
Tài liệu này được biên soạn nhằm giúp các em học sinh lớp 11 trường THPT Trần Phú củng cố kiến thức, kỹ năng đã học trong chương trình Toán 11, từ đó chuẩn bị tốt cho kì thi giữa học kì 2 sắp tới.
Nội Dung Ôn Tập:
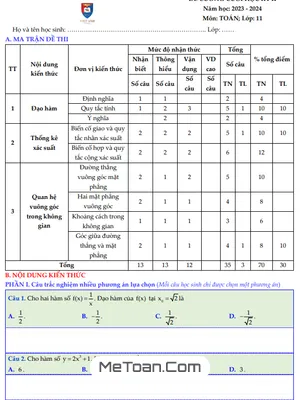
A. Phần Trắc Nghiệm:
- Chương 3: Dãy Số, Cấp Số Cộng và Cấp Số Nhân:
- Ôn tập về dãy số, cách tìm số hạng tổng quát, tính chất của dãy số.
- Cấp số cộng: Định nghĩa, số hạng tổng quát, tính chất, tổng n số hạng đầu tiên.
- Cấp số nhân: Định nghĩa, số hạng tổng quát, tính chất, tổng n số hạng đầu tiên.
- Chương 4: Giới Hạn:
- Giới hạn dãy số: Định nghĩa, các định lý về giới hạn, các dạng toán tính giới hạn.
- Giới hạn hàm số: Định nghĩa, các định lý về giới hạn, các dạng toán tính giới hạn, giới hạn một bên.
- Hàm số liên tục: Định nghĩa, các định lý về hàm số liên tục, các dạng toán xét tính liên tục của hàm số.
- Chương 5: Vectơ Trong Không Gian:
- Các khái niệm cơ bản về vectơ trong không gian: vectơ, độ dài vectơ, hai vectơ bằng nhau, ...
- Các phép toán trên vectơ trong không gian: cộng, trừ vectơ, nhân vectơ với một số, tích vô hướng của hai vectơ.
- Điều kiện đồng phẳng của ba vectơ.
B. Phần Tự Luận:
Chương 3: Chứng minh dãy số là cấp số cộng, cấp số nhân. Tìm công sai, công bội. Tính tổng n số hạng đầu tiên của cấp số cộng, cấp số nhân. Giải bài toán thực tế áp dụng công thức cấp số cộng, cấp số nhân.
Chương 4: Tính giới hạn của dãy số, giới hạn hàm số. Xét tính liên tục của hàm số.
Chương 5: Chứng minh ba vectơ đồng phẳng. Tìm tọa độ vectơ, độ dài vectơ, góc giữa hai vectơ.
Đề cương ôn tập mang tính chất tham khảo, học sinh cần kết hợp với việc học tập trên lớp, làm bài tập trong sách giáo khoa và sách bài tập.
Nên luyện tập thêm các dạng bài tập nâng cao để nắm vững kiến thức và đạt kết quả cao trong kì thi.
Chúc các em ôn tập tốt!