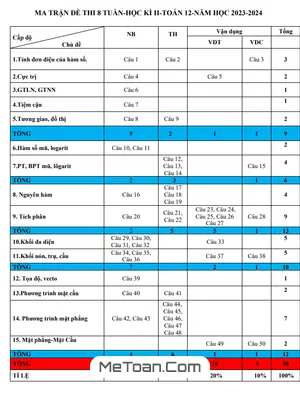
Đề thi giữa kỳ 2 Toán 12 năm 2020 - 2021 trường THPT Cam Lộ - Quảng Trị

Đề thi giữa kỳ 2 Toán 12 năm 2020 - 2021 trường THPT Cam Lộ - Quảng Trị

Đề thi giữa kỳ 2 Toán 12 năm học 2020 - 2021 trường THPT Cam Lộ – Quảng Trị được biên soạn theo hình thức trắc nghiệm với 50 câu hỏi trên 06 trang, thời gian làm bài 90 phút. Đề thi có đáp án mã đề 001.

Dưới đây là nội dung chi tiết của đề thi:

Nội dung:

1. Khái niệm nguyên hàm.
2. Công thức nguyên hàm cơ bản.
3. Tính chất nguyên hàm.
4. Nguyên hàm của hàm đa thức.
5. Nguyên hàm của hàm lượng giác.
6. Nguyên hàm của hàm mũ.
7. Nguyên hàm của hàm phân thức.
8. Phương pháp đổi biến số (tìm nguyên hàm).
9. Phương pháp nguyên hàm từng phần.
10. Bài nguyên hàm vận dụng cao.
11. Định nghĩa tích phân.
12. Tính chất tích phân.
13. Công thức bắc cầu (tích phân).
14. Tích phân hàm đa thức.
15. Tích phân hàm lượng giác.
16. Tích phân hàm chứa căn.
17. Phương pháp đổi biến số (tính tích phân).
18. Tính tích phân bằng phương pháp từng phần.
19. Bài toán tích phân vận dụng cao, ví dụ: tích phân hàm ẩn.
20. Lý thuyết ứng dụng tích phân tính diện tích hình phẳng.
21. Lý thuyết ứng dụng tích phân tính thể tích khối tròn xoay.
22. Nêu công thức tính diện tích hình phẳng khi cho trước hình ảnh đồ thị hàm f(x) trên đoạn [a,b].
23. Tính diện tích hình phẳng giới hạn bởi đồ thị y = f(x), y = 0, x = a, x = b.
24. Tính diện tích hình phẳng giới hạn bởi đồ thị y = f(x), y = g(x), x = a, x = b.
25. Tính thể tích khối tròn xoay giới hạn bởi đồ thị y = f(x), y = 0, x = a, x = b.
26. Tính diện tích hình phẳng giới hạn bởi đồ thị y = f(x), y = g(x).
27. Bài toán vận dụng cao, ví dụ: bài toán thực tế tính thể tích của chiếc trống trường.
28. Định nghĩa số phức.
29. Phần ảo số phức.
30. Phần thực số phức.
31. Số phức liên hợp.
32. Điểm biểu diễn số phức.
33. Hai số phức bằng nhau.
34. Tìm tập hợp điểm biểu diễn số phức.
35. Bài toán số phức vận dụng cao, ví dụ: bài toán cực trị liên quan đến quỹ tích tập hợp điểm biểu diễn số phức.
36. Tính tọa độ vecto theo định nghĩa.
37. Tính tổng, hiệu của các vecto.
38. Tính độ dài của vecto.
39. Tọa độ vecto tạo bởi hai điểm M, N.
40. Tìm tham số m để ba điểm A, B, C thẳng hàng.
41. Viết phương trình mặt cầu khi biết đường kính AB.
42. Viết phương trình mặt cầu đi qua 4 điểm A, B, C, D.
43. Bài toán vận dụng cao, ví dụ: Tìm tâm của đường tròn ngoại tiếp tam giác (thường) ABC.
44. Tìm vector pháp tuyến của mặt phẳng.
45. Tìm điểm thuộc mặt phẳng.
46. Viết phương trình mặt phẳng đi qua điểm M và có vector pháp tuyến cho trước.
47. Phương trình đoạn chắn (mặt phẳng).
48. Viết phương trình mặt phẳng đi qua 3 điểm A, B, C.
49. Tìm tọa độ hình chiếu vuông góc của M lên một trong ba mặt phẳng tọa độ.
50. Viết phương trình mặt phẳng đi qua điểm M và vuông góc với hai mặt phẳng (P) và (Q).