Đề Cương Ôn Tập Học Kỳ 2 Môn Toán Lớp 11 Năm 2022 - 2023 Trường THPT Yên Hòa - Hà Nội

Đề Cương Ôn Tập Kiểm Tra Học Kỳ 2 Môn Toán 11 Năm 2022-2023 - Trường THPT Yên Hòa - Hà Nội

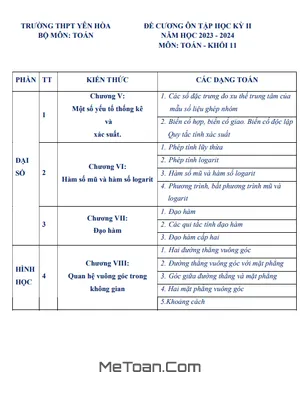
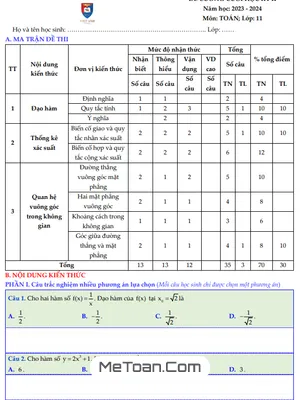
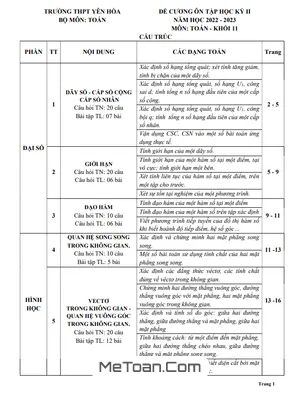
MeToan.Com chia sẻ đến quý thầy, cô giáo và các em học sinh lớp 11 tài liệu đề cương hướng dẫn ôn tập kiểm tra học kỳ 2 môn Toán 11 năm học 2022 – 2023 trường THPT Yên Hòa, quận Cầu Giấy, thành phố Hà Nội.

Tài liệu gồm 2 phần chính: Đại số và Giải tích 11, Hình học 11.

A. ĐẠI SỐ VÀ GIẢI TÍCH 11:

1. DÃY SỐ - CẤP SỐ CỘNG - CẤP SỐ NHÂN: (20 câu hỏi trắc nghiệm - 07 bài tập tự luận)

• Xác định số hạng tổng quát; xét tính tăng giảm, tính bị chặn của một dãy số.
• Xác định số hạng tổng quát, số hạng U1, công sai d; tính tổng n số hạng đầu tiên của một cấp số cộng.
• Xác định số hạng tổng quát, số hạng U1, công bội q; tính tổng n số hạng đầu tiên của một cấp số nhân.
• Vận dụng cấp số cộng, cấp số nhân vào một số bài toán ứng dụng thực tế.

2. GIỚI HẠN: (20 câu hỏi trắc nghiệm - 06 câu hỏi tự luận)

• Tính giới hạn của một dãy số.
• Tính giới hạn của một hàm số tại một điểm, tại vô cực; tính giới hạn một bên.
• Xét tính liên tục của hàm số tại một điểm, trên một tập cho trước.
• Xét sự tồn tại nghiệm của một phương trình.

3. ĐẠO HÀM: (10 câu hỏi trắc nghiệm - 06 câu hỏi tự luận)

• Tính đạo hàm của một hàm số tại một điểm.
• Tính đạo hàm của một hàm số trên tập xác định.
• Viết phương trình tiếp tuyến của đồ thị hàm số khi biết hoành độ tiếp điểm, hệ số góc.

B. HÌNH HỌC 11:

4. QUAN HỆ SONG SONG TRONG KHÔNG GIAN: (10 câu hỏi trắc nghiệm - 5 bài tập tự luận)

• Xác định và chứng minh hai mặt phẳng song song.
• Một số bài toán sử dụng tính chất của hai mặt phẳng song song.

5. VECTƠ TRONG KHÔNG GIAN – QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN: (20 câu hỏi trắc nghiệm - 12 bài tập tự luận)

• Xác định các đẳng thức véctơ, các tính chất đúng về véctơ trong không gian.
• Chứng minh hai đường thẳng vuông góc, đường thẳng vuông góc với mặt phẳng, hai mặt phẳng vuông góc trong không gian.
• Xác định và tính số đo góc: giữa hai đường thẳng, giữa đường thẳng và mặt phẳng, giữa hai mặt phẳng.
• Tính khoảng cách: từ một điểm đến mặt phẳng, giữa hai đường thẳng chéo nhau, giữa đường thẳng và mặt phẳng song song.
• Xác định và tính diện tích thiết diện cắt bởi mặt phẳng có quan hệ vuông góc.