Đề cương ôn tập học kì 1 Toán 11 năm 2019 - 2020 trường Đa Phúc - Hà Nội

MeToan.Com giới thiệu đến quý thầy, cô giáo và các em học sinh khối 11 đề cương ôn tập học kì 1 Toán 11 năm học 2019 - 2020 trường THPT Đa Phúc - Hà Nội. Đề cương gồm 16 trang trình bày nội dung kiến thức Toán 11 cần nắm và tuyển chọn các bài tập trắc nghiệm và tự luận Toán 11 để học sinh tự ôn tập, chuẩn bị cho kỳ thi HK1 Toán 11 năm học 2019 - 2020.

Khái quát nội dung đề cương ôn tập học kì 1 Toán 11 năm 2019 - 2020 trường Đa Phúc - Hà Nội:

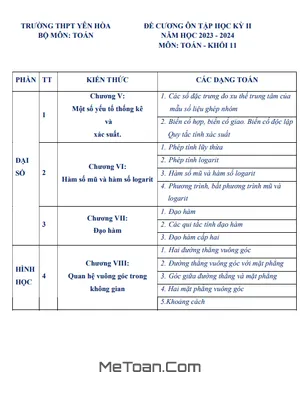
A. NỘI DUNG ÔN TẬP

I. Hàm số lượng giác và phương trình lượng giác.

1. Hàm số lượng giác.
2. Phương trình lượng giác cơ bản.
3. Một số phương trình lượng giác thường gặp.

II. Tổ hợp - Xác suất.

1. Quy tắc đếm.
2. Hoán vị - Chỉnh hợp - Tổ hợp.
3. Nhị thức Niu - tơn.
4. Phép thử và biến cố.
5. Xác suất của biến cố.

III. Dãy số - Cấp số cộng - Cấp số nhân.

1. Phương pháp quy nạp toán học.
2. Dãy số.
3. Cấp số cộng.
4. Cấp số nhân.

IV. Phép dời hình và phép đồng dạng.

1. Phép tịnh tiến.
2. Phép quay.
3. Phép vị tự.
4. Phép dời hình.
5. Phép đồng dạng.

V. Đường thẳng và mặt phẳng trong không gian. Quan hệ song song.

1. Bài toán tìm giao tuyến, giao điểm, thiết diện.
2. Chứng minh hai đường thẳng song song, đường thẳng song song với mặt phẳng, hai mặt phẳng song song.

[ads]

B. BÀI TẬP

• Cho tập hợp X = {0,1,2,3,4,5,6,7,8}. Từ các phần tử của tập X có thể lập bao nhiêu số tự nhiên trong mỗi trường hợp sau: a) Có 4 chữ số. b) Có 4 chữ số khác nhau. c) Là số chẵn và có 4 chữ số khác nhau. d) Có 4 chữ số đôi một khác nhau và luôn có mặt chữ số 1. e) Có 5 chữ số đôi một khác nhau và không bắt đầu bằng 123. f) Có 5 chữ số và chữ số đứng sau luôn lớn hơn chữ số đứng trước. g) Có 5 chữ số đôi một khác nhau và trong đó có 3 chữ số đầu chẵn, 2 chữ số cuối lẻ. h) Số có 4 chữ số đôi một khác nhau và lớn hơn 8600?

• Lớp 11A trường THPT Đa Phúc (Hà Nội) có 45 học sinh. Để đẩy mạnh phong trào học tập của lớp, lớp tổ chức 2 nhóm học tập là nhóm Toán và nhóm Tiếng Anh. Có 28 bạn tham gia nhóm Toán, 15 bạn tham gia nhóm tiếng Anh và 10 bạn không tham gia vào nhóm nào. Hỏi có bao nhiêu bạn tham gia cả 2 nhóm.

• Cho tứ diện ABCD, gọi M, N lần lượt là trung điểm của các cạnh AD và BC, G là trọng tâm của tam giác BCD. Khi đó, giao điểm của đường thẳng MG với (ABC) là? A. Giao điểm của đường thẳng MG và đường thẳng BC. B. Giao điểm của đường thẳng MG và đường thẳng AC. C. Điểm N. D. Giao điểm của đường thẳng MG và đường thẳng AN.