Đề cương học kỳ 1 Toán lớp 11 năm 2023 - 2024 trường THPT Hoàng Văn Thụ - Hà Nội

Đề cương ôn tập học kỳ 1 Toán 11 năm 2023 - 2024 trường THPT Hoàng Văn Thụ - Hà Nội

MeToan.Com giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 11 đề cương ôn tập kiểm tra cuối học kỳ 1 môn Toán 11 năm học 2023 – 2024 trường THPT Hoàng Văn Thụ, quận Hoàng Mai, thành phố Hà Nội.

1. Kiến thức

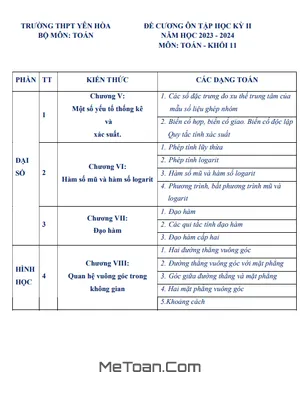
1.1. Đại số

Góc lượng giác và các giá trị lượng giác của một góc lượng giác. Công thức lượng giác. Hàm số lượng giác. Phương trình lượng giác.
Dãy số - Cấp số cộng - Cấp số nhân.
Giới hạn của dãy số. Giới hạn của hàm số. Hàm số liên tục.
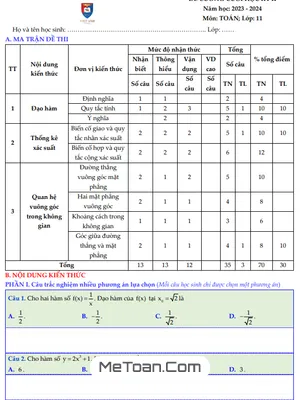
Mẫu số liệu ghép nhóm và các số đặc trưng đo xu thế trung tâm của mẫu số liệu ghép nhóm.

1.2. Hình học

Đường thẳng và mặt phẳng trong không gian.
Hai đường thẳng song song.
Đường thẳng và mặt phẳng song song.
Hai mặt phẳng song song.
Phép chiếu song song.

2. Kĩ năng

2.1. Đại số

Tính được giá trị lượng giác của 1 góc lượng giác.
Tìm mối liên hệ giữa các giá trị lượng giác của các góc liên quan đặc biệt.
Tìm tập xác định của hàm số lượng giác.
Tìm chu kì, xét tính chẵn lẻ, tính đồng biến, nghịch biến của một hàm số lượng giác.
Biến đổi các công thức lượng giác.
Giải phương trình lượng giác cơ bản.
Giải các bài toán thực tế liên quan đến góc lượng giác, công thức lượng giác, hàm số lượng giác.
Tìm số hạng của 1 dãy số. Xét tính tăng, giảm, bị chặn của 1 dãy số.
Nhận biết 1 cấp số cộng. Tìm công sai, số hạng tổng quát, tổng n số hạng đầu của một cấp số cộng.
Nhận biết 1 cấp số nhân. Tìm công sai, số hạng tổng quát, tổng n số hạng đầu của một cấp số nhân.
Dùng kiến thức về dãy số, cấp số cộng, cấp số nhân để giải quyết một số bài toán thực tế.
Tính giới hạn của dãy số, tính giới hạn hàm số.
Xét tính liên tục của hàm số. Tìm điều kiện của tham số để hàm số liên tục tại một điểm.
Lập bảng phân bố tần số ghép nhóm từ 1 mẫu số liệu.
Tính các số đặc trưng đo độ phân tán của mẫu số liệu ghép nhóm.

2.2. Hình học

Tìm giao tuyến của hai mặt phẳng.
Tìm giao điểm của đường thẳng và mặt phẳng.
Chứng minh hai đường thẳng song song, đường thẳng song song mặt phẳng, hai mặt phẳng song song..