Đề Cương Học Kì 1 Toán 11 Năm 2025 – 2026 Trường THPT Xuân Phương – Hà Nội

MeToan.Com xin trân trọng giới thiệu đến quý thầy, cô giáo và các em học sinh Đề cương ôn tập kiểm tra cuối học kì 1 môn Toán 11 năm học 2025 – 2026 của trường THPT Xuân Phương, thành phố Hà Nội. Tài liệu này được biên soạn nhằm tổng hợp và hệ thống hóa kiến thức trọng tâm, cùng với các dạng bài tập tiêu biểu, giúp các em chuẩn bị tốt nhất cho kì thi sắp tới.

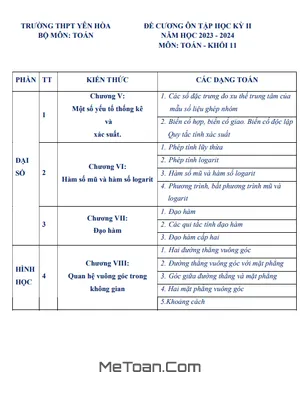
A. KIẾN THỨC TRỌNG TÂM

Chương I. Hàm số lượng giác và phương trình lượng giác.

• Giá trị lượng giác của góc lượng giác: Nắm vững định nghĩa các giá trị sin, cos, tan, cot, đường tròn lượng giác và các cung đặc biệt. Hiểu rõ cách xác định dấu và giá trị của các hàm số lượng giác trên các góc khác nhau.
• Công thức lượng giác: Thành thạo các công thức cơ bản, công thức cộng, nhân đôi, hạ bậc, biến đổi tổng thành tích và tích thành tổng. Vận dụng linh hoạt các công thức để rút gọn biểu thức và giải các bài toán liên quan.
• Hàm số lượng giác: Khảo sát tập xác định, tập giá trị, chu kì, tính chẵn lẻ, và đồ thị của các hàm số lượng giác cơ bản (y = sinx, y = cosx, y = tanx, y = cotx). Hiểu rõ sự biến thiên và các đặc điểm của đồ thị.
• Phương trình lượng giác: Giải các phương trình lượng giác cơ bản (sinx = m, cosx = m, tanx = m, cotx = m) và các dạng phương trình thường gặp khác như phương trình bậc nhất, bậc hai đối với một hàm số lượng giác, hoặc phương trình đẳng cấp.

Chương II. Dãy số. Cấp số cộng và cấp số nhân.

• Dãy số: Hiểu khái niệm dãy số, cách xác định (bằng công thức số hạng tổng quát hoặc công thức truy hồi). Biết cách tìm số hạng, khảo sát tính đơn điệu và tính bị chặn của dãy số.
• Cấp số cộng: Nắm vững định nghĩa, công thức số hạng tổng quát u_n = u_1 + (n-1)d, công thức tính tổng n số hạng đầu tiên S_n = n/2 * (u_1 + u_n) hoặc S_n = n/2 * [2u_1 + (n-1)d]. Giải các bài toán liên quan đến tìm số hạng, công sai, và tổng các số hạng.
• Cấp số nhân: Nắm vững định nghĩa, công thức số hạng tổng quát u_n = u_1 * q^(n-1), công thức tính tổng n số hạng đầu tiên S_n = u_1 * (1-q^n) / (1-q) (với q ≠ 1). Giải các bài toán liên quan đến tìm số hạng, công bội, và tổng các số hạng.

Chương III. Các số đặc trưng đo xu thế trung tâm của mẫu số liệu ghép nhóm.

• Mẫu số liệu ghép nhóm: Nắm vững cách lập bảng tần số – tần suất ghép nhóm từ dữ liệu thô và ý nghĩa của các khoảng nhóm, tần số, tần suất tương ứng.
• Các số đặc trưng đo xu thế trung tâm: Hiểu và biết cách tính toán, diễn giải số trung bình cộng, trung vị, tứ phân vị, mốt cho mẫu số liệu ghép nhóm để đánh giá xu thế tập trung của dữ liệu. So sánh và phân tích ý nghĩa của từng số đặc trưng.

Chương IV. Quan hệ song song trong không gian.

• Đường thẳng và mặt phẳng trong không gian: Các khái niệm cơ bản về điểm, đường thẳng, mặt phẳng. Nắm vững các tiên đề hình học không gian và kỹ năng vẽ hình biểu diễn các hình không gian đúng quy ước.
• Hai đường thẳng song song: Định nghĩa, các tính chất và các định lý liên quan đến hai đường thẳng song song trong không gian. Biết cách chứng minh sự song song của hai đường thẳng.
• Đường thẳng và mặt phẳng song song: Định nghĩa, các định lý và hệ quả. Hiểu rõ các phương pháp chứng minh đường thẳng song song với mặt phẳng và ứng dụng trong việc tìm giao tuyến, thiết diện.
• Hai mặt phẳng song song: Định nghĩa, các tính chất và cách chứng minh sự song song của hai mặt phẳng. Áp dụng vào các bài toán liên quan đến thiết diện song song, khoảng cách giữa các mặt phẳng.

Chương V. Giới hạn. Hàm số liên tục.

• Giới hạn của dãy số: Nắm vững khái niệm giới hạn hữu hạn và vô hạn của dãy số. Các định lý về giới hạn của tổng, hiệu, tích, thương. Các phương pháp tìm giới hạn dãy số, bao gồm các dạng vô định và cách khử dạng vô định.
• Giới hạn của hàm số: Hiểu khái niệm giới hạn của hàm số tại một điểm, giới hạn một phía, giới hạn tại vô cực. Áp dụng các định lý về giới hạn của hàm số và các phương pháp tính giới hạn, bao gồm cả biến đổi đại số để khử dạng vô định.
• Hàm số liên tục: Định nghĩa hàm số liên tục tại một điểm và trên một khoảng. Nắm vững các định lý về hàm số liên tục (tổng, hiệu, tích, thương của các hàm liên tục) và ứng dụng của tính liên tục để chứng minh sự tồn tại nghiệm của phương trình trên một khoảng cho trước.

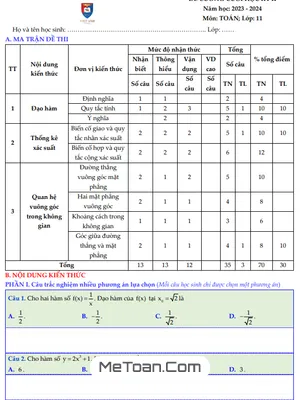
B. BÀI TẬP. Phần bài tập được biên soạn đa dạng, bao gồm cả tự luận và trắc nghiệm, bám sát theo từng chủ đề kiến thức, giúp các em củng cố lý thuyết và rèn luyện kỹ năng giải toán, chuẩn bị hiệu quả cho kì thi.