Đề cương giữa kì 2 Toán 11 năm 2024 - 2025 trường THPT Nguyễn Việt Hồng - Cần Thơ

Đề cương ôn tập giữa kì 2 môn Toán 11 năm học 2024 - 2025 trường THPT Nguyễn Việt Hồng - Cần Thơ

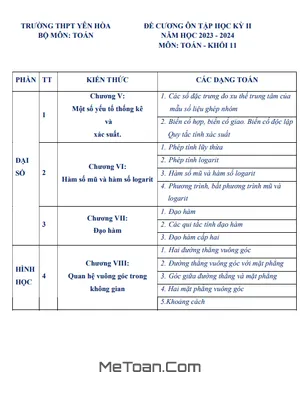
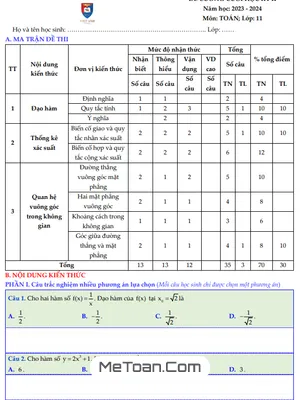
MeToan.Com giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 11 đề cương ôn tập kiểm tra giữa học kì 2 môn Toán 11 năm học 2024 – 2025 trường THPT Nguyễn Việt Hồng, thành phố Cần Thơ.

1.1. Phân tích và xử lí dữ liệu.

• Tính được các số đặc trưng đo xu thế trung tâm cho mẫu số liệu ghép nhóm: số trung bình cộng (hay số trung bình), trung vị (median), tứ phân vị (quartiles), mốt (mode).
• Hiểu được ý nghĩa và vai trò của các số đặc trưng nói trên của mẫu số liệu trong thực tiễn.
• Rút ra được kết luận nhờ ý nghĩa của các số đặc trưng nói trên của mẫu số liệu trong trường hợp đơn giản.
• Nhận biết được mối liên hệ giữa thống kê với những kiến thức của các môn học khác trong Chương trình lớp 11 và trong thực tiễn.

1.2. Khái niệm về xác suất. Các quy tắc tính xác suất.

• Nhận biết được một số khái niệm về xác suất cổ điển: hợp và giao các biến cố; biến cố độc lập.
• Tính được xác suất của biến cố hợp bằng cách sử dụng công thức cộng.
• Tính được xác suất của biến cố giao bằng cách sử dụng công thức nhân (cho trường hợp biến cố độc lập).
• Tính được xác suất của biến cố trong một số bài toán đơn giản bằng phương pháp tổ hợp.
• Tính được xác suất trong một số bài toán đơn giản bằng cách sử dụng sơ đồ hình cây.

1.3. Phép tính luỹ thừa với số mũ thực.

• Nhận biết được khái niệm luỹ thừa với số mũ nguyên của một số thực khác 0; luỹ thừa với số mũ hữu tỉ và luỹ thừa với số mũ thực của một số thực dương.
• Giải thích được các tính chất của phép tính luỹ thừa với số mũ nguyên, luỹ thừa với số mũ hữu tỉ và luỹ thừa với số mũ thực.
• Sử dụng được tính chất của phép tính luỹ thừa trong tính toán các biểu thức số và rút gọn các biểu thức chứa biến (tính viết và tính nhẩm, tính nhanh một cách hợp lí).
• Tính được giá trị biểu thức số có chứa phép tính luỹ thừa bằng sử dụng máy tính cầm tay.
• Giải quyết được một số vấn đề có liên quan đến môn học khác hoặc có liên quan đến thực tiễn gắn với phép tính luỹ thừa (ví dụ: bài toán về lãi suất, sự tăng trưởng).

1.4. Quan hệ vuông góc trong không gian. Phép chiếu vuông góc.

1.4.1. Hai đường thẳng vuông góc.

• Nhận biết được khái niệm góc giữa hai đường thẳng trong không gian.
• Nhận biết được hai đường thẳng vuông góc trong không gian.
• Chứng minh được hai đường thẳng vuông góc trong không gian trong một số trường hợp đơn giản.
• Sử dụng được kiến thức về hai đường thẳng vuông góc để mô tả một số hình ảnh trong thực tiễn.

1.4.2. Đường thẳng vuông góc với mặt phẳng.

• Nhận biết được đường thẳng vuông góc với mặt phẳng.
• Xác định được điều kiện để đường thẳng vuông góc với mặt phẳng.
• Giải thích được định lí ba đường vuông góc.
• Giải thích được mối liên hệ giữa tính song song và tính vuông góc của đường thẳng và mặt phẳng.
• Nhận biết được khái niệm phép chiếu vuông góc.
• Xác định được hình chiếu vuông góc của một điểm, một đường thẳng, một tam giác.
• Nhận biết được công thức tính thể tích của hình chóp, hình lăng trụ, hình hộp.
• Tính được thể tích của hình chóp, hình lăng trụ, hình hộp trong những trường hợp đơn giản (ví dụ: nhận biết được đường cao và diện tích mặt đáy của hình chóp).
• Vận dụng được kiến thức về đường thẳng vuông góc với mặt phẳng để mô tả một số hình ảnh trong thực tiễn.

1.4.3. Góc giữa đường thẳng và mặt phẳng. Góc nhị diện.

• Nhận biết được khái niệm góc giữa đường thẳng và mặt phẳng.
• Xác định và tính được góc giữa đường thẳng và mặt phẳng trong những trường hợp đơn giản (ví dụ: đã biết hình chiếu vuông góc của đường thẳng lên mặt phẳng).
• Nhận biết được khái niệm góc nhị diện, góc phẳng nhị diện.
• Xác định và tính được số đo góc nhị diện, góc phẳng nhị diện trong những trường hợp đơn giản (ví dụ: nhận biết được mặt phẳng vuông góc với cạnh nhị diện).
• Sử dụng được kiến thức về góc giữa đường thẳng và mặt phẳng, góc nhị diện để mô tả một số hình ảnh trong thực tiễn.