Đề Thi Giữa Học Kỳ 1 Môn Toán Lớp 12 Năm 2025 - 2026 Sở GD&ĐT Hưng Yên (Có Đáp Án)

Để chuẩn bị tốt nhất cho kỳ kiểm tra giữa học kỳ 1 sắp tới, MeToan.Com xin gửi đến quý thầy cô giáo và các em học sinh lớp 12 một tài liệu tham khảo chất lượng: bộ đề khảo sát môn Toán của Sở Giáo dục và Đào tạo tỉnh Hưng Yên, năm học 2025 – 2026. Kỳ thi chính thức được tổ chức vào ngày 01/11/2025.
Cấu Trúc Đề Thi Mới Nhất
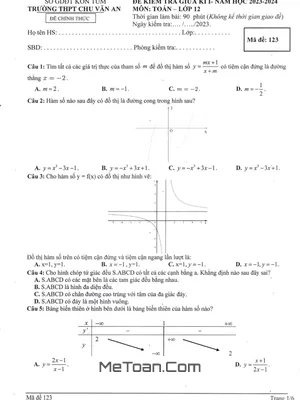
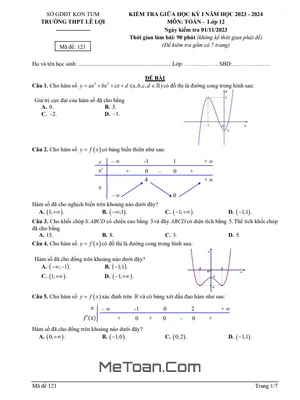
Đề thi được biên soạn theo định hướng phát triển năng lực của chương trình giáo dục phổ thông mới, với thời gian làm bài là 90 phút. Cấu trúc đề bao gồm ba phần chính, đòi hỏi học sinh phải có kỹ năng làm bài đa dạng:
- Phần 1: 12 câu hỏi trắc nghiệm khách quan với 4 phương án lựa chọn.
- Phần 2: 04 câu hỏi trắc nghiệm dạng Đúng – Sai, yêu cầu học sinh phải phân tích và đánh giá tính chính xác của từng mệnh đề.
- Phần 3: 06 câu hỏi trắc nghiệm yêu cầu trả lời ngắn, học sinh cần điền kết quả cuối cùng vào phiếu trả lời.
Bộ đề thi được cung cấp đầy đủ đáp án cho tất cả các mã đề, giúp các em dễ dàng đối chiếu kết quả và tự đánh giá năng lực sau khi làm bài.
Phân Tích Một Số Dạng Toán Vận Dụng Cao Tiêu Biểu
Trong đề thi có nhiều câu hỏi vận dụng và vận dụng cao, tập trung vào các chủ đề quan trọng của chương trình Toán 12. Dưới đây là một số ví dụ điển hình:
Bài toán xác suất tổ hợp: Một câu hỏi yêu cầu tính xác suất chọn được một tam giác cân nhưng không phải tam giác đều từ tập hợp các tam giác có đỉnh là đỉnh của một đa giác đều 12 đỉnh nội tiếp đường tròn. Đây là dạng toán kết hợp giữa hình học và tổ hợp, đòi hỏi sự tư duy logic và tính toán cẩn thận.
Bài toán ứng dụng thực tế của Parabol: Một bài toán tối ưu hóa liên quan đến việc vận chuyển một thùng hàng hình hộp chữ nhật qua một chiếc cổng hình Parabol. Học sinh cần áp dụng kiến thức về phương trình Parabol và khảo sát hàm số để tìm diện tích mặt cắt lớn nhất có thể.
Bài toán ứng dụng đạo hàm trong kinh tế: Đề bài đưa ra một mô hình tăng trưởng doanh số theo hàm logistic và yêu cầu xác định doanh số tại thời điểm tốc độ bán hàng đạt mức cao nhất. Đây là một dạng toán ứng dụng thực tế của đạo hàm để tìm điểm cực trị, giúp học sinh thấy được sự liên kết giữa toán học và cuộc sống.