Đề Cương Ôn Tập Giữa Kỳ 1 Toán 12 Năm Học 2025

Nhằm hỗ trợ các em học sinh lớp 12 chuẩn bị tốt nhất cho kỳ kiểm tra giữa học kỳ 1 sắp tới, tài liệu đề cương ôn tập môn Toán 12 năm học 2025 – 2026 của trường THPT Quế Sơn, Đà Nẵng đã được biên soạn chi tiết và hệ thống. Đây là nguồn tài liệu quan trọng, giúp các em củng cố kiến thức nền tảng và rèn luyện kỹ năng giải các dạng bài tập trọng tâm.

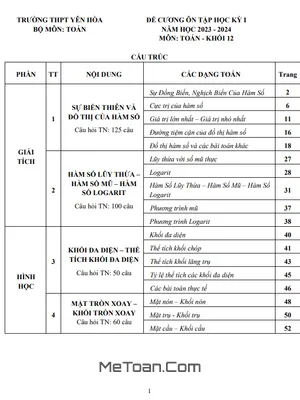
Nội dung chính của đề cương tập trung vào chương đầu tiên của chương trình Giải tích 12, một trong những phần kiến thức cốt lõi và thường xuất hiện trong các kỳ thi quan trọng. Cụ thể, các chuyên đề học sinh cần nắm vững bao gồm:

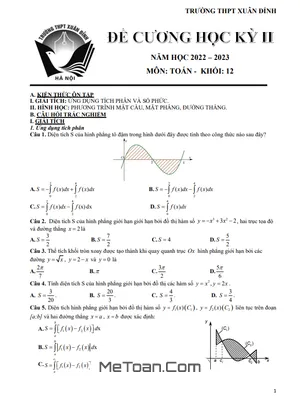
CHUYÊN ĐỀ: ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ

Đây là chương kiến thức nền tảng, chiếm tỷ trọng điểm số cao trong bài thi. Các em cần tập trung ôn luyện kỹ lưỡng các nội dung sau:

Tính đơn điệu của hàm số: Phần này yêu cầu học sinh phải thành thạo kỹ năng tính đạo hàm và xét dấu của đạo hàm (y'). Từ đó, các em có thể kết luận chính xác các khoảng đồng biến, nghịch biến của hàm số, một bước không thể thiếu trong quá trình khảo sát hàm số.
Giá trị lớn nhất và giá trị nhỏ nhất (GTLN - GTNN) của hàm số: Dạng toán này tập trung vào việc tìm kiếm giá trị lớn nhất và nhỏ nhất của một hàm số trên một tập xác định cho trước, chẳng hạn như một đoạn [a; b], một khoảng hoặc trên toàn bộ tập xác định. Kỹ năng giải phương trình y' = 0 và lập bảng biến thiên là yếu tố then chốt để giải quyết các bài toán này.
Khảo sát sự biến thiên và vẽ đồ thị hàm số: Đây là nội dung tổng hợp, yêu cầu vận dụng tất cả kiến thức đã học như tìm tập xác định, tính đạo hàm, tìm cực trị, xét tính đơn điệu, tìm tiệm cận (đối với hàm phân thức) và lập bảng biến thiên. Từ đó, học sinh có thể phác họa chính xác đồ thị của các dạng hàm số quen thuộc như hàm bậc ba, hàm bậc bốn trùng phương và hàm hữu tỉ bậc nhất trên bậc nhất.
Ứng dụng đạo hàm trong giải quyết các bài toán thực tiễn: Đây là phần vận dụng cao, giúp học sinh thấy được sự liên kết giữa Toán học và cuộc sống. Các bài toán thường liên quan đến tối ưu hóa chi phí, tối đa hóa lợi nhuận, hoặc tìm kích thước tối ưu để có thể tích, diện tích lớn nhất. Việc mô hình hóa bài toán và sử dụng công cụ đạo hàm để giải quyết là kỹ năng quan trọng cần rèn luyện.

Việc ôn tập kỹ lưỡng theo đề cương này sẽ giúp các em học sinh trường THPT Quế Sơn tự tin hơn và đạt được kết quả cao trong kỳ thi giữa kỳ 1.