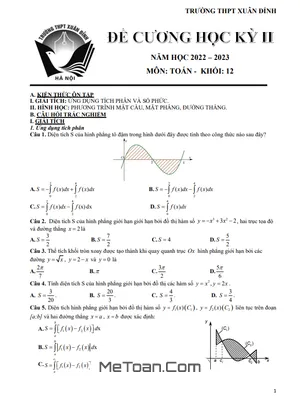
Đề cương học kỳ 2 Toán 12 năm 2022 - 2023 trường THPT Bắc Thăng Long - Hà Nội

Đề cương ôn tập học kỳ 2 Toán 12 năm 2022 - 2023 trường THPT Bắc Thăng Long - Hà Nội

MeToan.Com giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề cương ôn tập cuối học kỳ 2 môn Toán 12 năm học 2022 – 2023 trường THPT Bắc Thăng Long, thành phố Hà Nội.

Trích dẫn Đề cương học kỳ 2 Toán 12 năm 2022 – 2023 trường THPT Bắc Thăng Long – Hà Nội:

• Trong không gian với hệ tọa độ Oxyz, cho hai mặt cầu (S1), (S2) lần lượt có phương trình là x² + y² + z² − 2x − 2y − 2z − 22 = 0, x² + y² + z² − 6x + 4y + 2z + 5 = 0. Xét các mặt phẳng (P) thay đổi nhưng luôn tiếp xúc với cả hai mặt cầu đã cho. Gọi M (a; b; c) là điểm mà tất cả các mặt phẳng (P) đi qua. Tính tổng S = a + b + c.

• Cho hàm số có bảng xét dấu của đạo hàm như sau:

  x

  -∞

  1

  3

  5

  +∞

  f'(x)

  -

  0

  0

  -

  Đặt g(x) = f(x + 2) + 1/3x³ − 2x² + 3x + 2019. Khẳng định nào sau đây đúng?

  A. Hàm số y = g(x) đạt cực đại tại x = 1. 
  B. Hàm số y = g(x) có 1 điểm cực trị. 
  C. Hàm số y = g(x) nghịch biến trên khoảng (1; 4). 
  D. g(5) > g(6) và g(0) > g(1).  
  

• Ông An có một khu vườn giới hạn bởi đường parabol và đường thẳng. Nếu đặt trong hệ tọa độ Oxy như hình vẽ thì parabol có phương trình y = x² và đường thẳng là y = 25. Ông An dự định dùng một mảnh vườn nhỏ được chia từ khu vườn bởi đường thẳng đi qua điểm O và M trên parabol để trồng một loại hoa. Hãy giúp ông An xác định điểm M bằng cách tính độ dài OM để diện tích mảnh vườn nhỏ bằng 9/2.