Ứng dụng tích phân tính diện tích hình phẳng với dữ kiện thực tế

Tài liệu gồm 24 trang, được biên soạn bởi nhóm tác giả Toán Học Bắc Trung Nam, là tài liệu hữu ích cho học sinh lớp 12 đang ôn tập chương Nguyên hàm - Tích phân và ứng dụng. Tài liệu hướng dẫn giải các bài toán ứng dụng tích phân trong bài toán diện tích hình phẳng với dữ kiện toán thực tế, đây là dạng toán vận dụng cao (VDC) thường gặp trong chương trình Giải tích 12 chương 3: Nguyên hàm, tích phân và ứng dụng. Các bài toán trắc nghiệm trong tài liệu đều có đáp án và lời giải chi tiết.

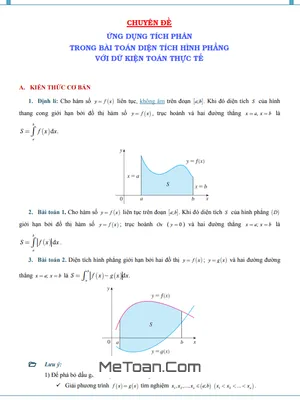
A. KIẾN THỨC CƠ BẢN

B. BÀI TẬP

1. NHỮNG BÀI TOÁN THỰC TẾ SỬ DỤNG ĐỒ THỊ HÀM PARABOL.

Bước 1. Chọn hệ trục tọa độ, xác định parabol. Bước 2. Tính diện tích hình phẳng giới hạn đồ thị hàm số y = f(x) và các đường được cho trong bài toán. Bước 3. Tùy theo thực tế mỗi bài, tính diện tích theo yêu cầu.

Chú ý: Mấu chốt của vấn đề tính diện tích parabol nằm ở khâu chọn hệ trục tọa độ phù hợp. Nên chọn hệ trục sao cho đỉnh parabol luôn nằm trùng với gốc O hoặc nằm trên trục Oy. Khi đó hàm số parabol luôn có dạng y = ax^2 + b.

DẠNG 1: CÁC BÀI TOÁN TÍNH DIỆN TÍCH PARABOL ĐƠN THUẦN.

DẠNG 2: CÁC BÀI TOÁN TÍNH DIỆN TÍCH XÁC ĐỊNH BỞI HAI HÀM SỐ.

2. NHỮNG BÀI TOÁN THỰC TẾ SỬ DỤNG ĐỒ THỊ HÀM ELIP.

Bước 1. Chọn hệ trục tọa độ, xác định Elip. Bước 2. Tính diện tích hình phẳng giới hạn đồ thị hàm số f(x) và các đường được cho trong bài toán. Bước 3. Tùy theo thực tế mỗi bài, tính diện tích theo yêu cầu.

Chú ý: Mấu chốt của vấn đề tính diện tích Elip nằm ở khâu chọn hệ trục tọa độ phù hợp. Nên chọn hệ trục sao cho tâm Elip luôn nằm trùng với gốc O. Khi đó phương trình Elip luôn có dạng x^2/a^2 + y^2/b^2 = 1.

3. NHỮNG BÀI TOÁN THỰC TẾ SỬ DỤNG ĐƯỜNG TRÒN.

Bước 1. Xác định Phương trình của đường tròn: (x-a)^2 + (y-b)^2 = R^2. Diện tích toàn phần của đường tròn: S = πR^2. Bước 2. Trên hệ trục tọa độ, đặt đường tròn và phác họa phần mặt phẳng cần tính diện tích được giới hạn bởi đồ thị hàm số y = f(x) và đường tròn. Bước 3. Ta sử dụng công thức tính diện tích ∫[a, b] (f(x) - g(x)) dx để tính diện tích phần cần tính. Bước 4. Tùy thuộc vào câu hỏi để kết luận và đưa ra kết quả bài toán.