Ứng Dụng Tích Phân Giải Bài Toán So Sánh Giá Trị Hàm Số

Tài liệu 16 trang do nhóm Toán Học Bắc Trung Nam biên soạn, hướng dẫn phương pháp ứng dụng tích phân để giải bài toán so sánh giá trị hàm số. Đây là dạng toán vận dụng cao (VDC) thường gặp trong chương trình Giải tích 12, chương 3: Nguyên hàm, tích phân và ứng dụng. Các bài toán trắc nghiệm trong tài liệu đều có đáp án và lời giải chi tiết.

Ví dụ minh họa:

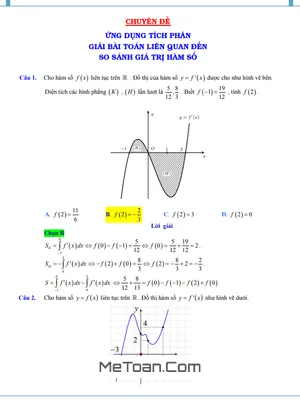
• Cho hàm số f(x) liên tục trên R. Đồ thị của hàm số y = f(x) được cho như hình vẽ bên. Diện tích các hình phẳng K, H lần lượt là 5, 8, 12, 3. Biết ∫1^19 f(x)dx = 12, tính f(2).
• Cho các số thực a, b, c, d thỏa mãn 0 < a < b < c < d và hàm số y = f(x). Biết hàm số y = f'(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y = f(x) trên [0; d]. Khẳng định nào sau đây là khẳng định đúng?
• Cho hàm số f(x) có đạo hàm là f'(x). Đồ thị của hàm số y = f'(x) được cho như hình bên. Biết rằng f(0) + f(2) + f(3) = f(5) = 3. Giá trị nhỏ nhất, giá trị lớn nhất của f(x) trên đoạn [0; 5] lần lượt là?
• Cho hàm số y = f(x) xác định và có đạo hàm trên R. Biết đồ thị hàm số y = f'(x) như hình vẽ bên. Xét hàm số g(x) = f²(x) + 2x. Tìm số lớn nhất trong ba số g(1), g(2), g(3)?
• Cho hàm số y = f(x) liên tục trên R, đồ thị của hàm số y = f'(x) có dạng như hình vẽ bên. Số nào lớn nhất trong các số sau: f(0), f(1), f(2), f(3)?