Trọn Bộ Chuyên Đề Toán 6 KNTT (Tập 2): Lý Thuyết và Bài Tập Cơ Bản

Tài liệu tổng hợp kiến thức trọng tâm và các dạng bài tập cốt lõi của môn Toán lớp 6 học kỳ 2, bám sát theo chương trình sách giáo khoa Kết Nối Tri Thức Với Cuộc Sống. Với dung lượng 113 trang, bộ chuyên đề này được biên soạn chi tiết, hệ thống hóa kiến thức một cách khoa học, giúp các em học sinh dễ dàng ôn tập và củng cố nền tảng.
Nội dung tài liệu bao quát 4 chương chính của học kỳ 2:
Chương VI: Phân Số Học sinh sẽ được tiếp cận sâu hơn về khái niệm phân số, từ việc mở rộng và nhận biết các phân số bằng nhau cho đến kỹ năng so sánh phân số và làm quen với hỗn số dương. Trọng tâm của chương là rèn luyện thành thạo bốn phép tính cơ bản: cộng, trừ, nhân, chia phân số. Đặc biệt, chuyên đề đi sâu vào hai dạng bài toán về phân số điển hình, giúp học sinh vận dụng kiến thức đã học để giải quyết các vấn đề thực tiễn.
Chương VII: Số Thập Phân Tiếp nối kiến thức về phân số, chương này giới thiệu về số thập phân và các quy tắc tính toán liên quan. Học sinh sẽ được hướng dẫn chi tiết cách thực hiện các phép tính với số thập phân, đồng thời nắm vững phương pháp làm tròn số và kỹ năng ước lượng kết quả. Nội dung chương còn đề cập đến các bài toán quan trọng về tỉ số và tỉ số phần trăm, một dạng toán có tính ứng dụng cao trong cuộc sống.
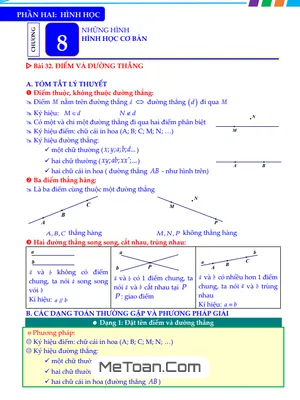
Chương VIII: Những Hình Học Cơ Bản Phần hình học trực quan cung cấp những khái niệm nền tảng nhất về điểm, đường thẳng, tia, và đoạn thẳng. Các em sẽ học cách xác định điểm nằm giữa, đo độ dài đoạn thẳng và tìm trung điểm của một đoạn thẳng. Bên cạnh đó, chuyên đề giới thiệu về góc và cách sử dụng thước đo để xác định số đo góc, tạo tiền đề vững chắc cho các kiến thức hình học phức tạp hơn ở các lớp trên.
Chương IX: Dữ Liệu và Xác Suất Thực Nghiệm Chương cuối cùng trang bị cho học sinh những kiến thức hiện đại và cần thiết về thống kê mô tả. Nội dung bao gồm phương pháp thu thập và phân loại dữ liệu, cách trình bày thông tin qua bảng thống kê, biểu đồ tranh, biểu đồ cột và biểu đồ cột kép. Ngoài ra, học sinh sẽ bắt đầu làm quen với các khái niệm về kết quả có thể xảy ra của một sự kiện và bước đầu tìm hiểu về xác suất thực nghiệm thông qua các trò chơi, thí nghiệm đơn giản.