Tóm Tắt Lý Thuyết Và Bài Tập Trắc Nghiệm So Sánh Phân Số, Hỗn Số Dương
Tóm Tắt Lý Thuyết Và Bài Tập Trắc Nghiệm So Sánh Phân Số, Hỗn Số Dương
MeToan.Com giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 6 tài liệu tóm tắt lý thuyết và bài tập trắc nghiệm chuyên đề so sánh phân số, hỗn số dương. Các bài toán được chọn lọc và phân loại theo các dạng toán, được sắp xếp theo độ khó từ cơ bản đến nâng cao, có đáp án và hướng dẫn giải chi tiết, giúp các em tham khảo khi học chương trình Toán 6.
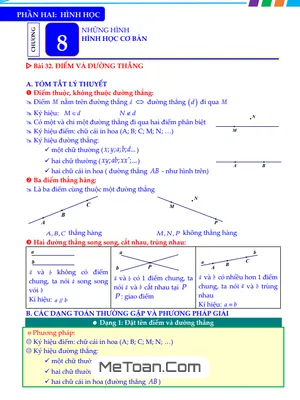
A. TÓM TẮT LÝ THUYẾT
I. QUY ĐỒNG MẪU NHIỀU PHÂN SỐ.
Để quy đồng mẫu hai hay nhiều phân số có mẫu số dương, ta làm như sau:
- Tìm một bội chung (thường là BCNN) của các mẫu để làm mẫu chung.
- Tìm thừa số phụ của mỗi mẫu bằng cách chia mẫu chung cho từng mẫu.
- Nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng.
II. SO SÁNH HAI PHÂN SỐ.
- So sánh hai phân số có cùng mẫu.
Trong hai phân số cùng một mẫu số dương, phân số nào có tử lớn hơn thì phân số đó lớn hơn.
- So sánh hai phân số không cùng mẫu.
Muốn so sánh hai phân số không cùng mẫu, ta viết chúng dưới dạng hai phân số có cùng một mẫu dương rồi so sánh tử với nhau: Phân số nào có tử lớn hơn thì phân số đó lớn hơn.
III. HỖN SỐ DƯƠNG.
- Hỗn số.
Một số có dạng a b/c được gọi là một hỗn số trong đó a là phần nguyên, b/c là phần phân số. Hỗn số a b/c được đọc là a b phần c (vd 2 3/4 đọc là Hai ba phần tư).
- Chuyển từ phân số sang hỗn số.
Muốn viết một phân số (lớn hơn 1) a/b trong đó a, b, c, d là các số nguyên dương và a > b (a chia b được thương c dư d) thì khi đó a/b = (bc + d)/b = c + d/b = c d/b.
- Chuyển từ hỗn số sang phân số.
Muốn viết một hỗn số a b/c về dạng một phân số ta làm như sau: a b/c = (a.c + b)/c.
B. BÀI TẬP TRẮC NGHIỆM
I – MỨC ĐỘ NHẬN BIẾT.
II – MỨC ĐỘ THÔNG HIỂU.
III – MỨC ĐỘ VẬN DỤNG.
IV – MỨC ĐỘ VẬN DỤNG CAO.
