Tài Liệu Dạy Thêm - Học Thêm Chuyên Đề Thứ Tự Thực Hiện Phép Tính Lớp 6

Tài liệu gồm 17 trang, tổng hợp tóm tắt lý thuyết, hướng dẫn phương pháp giải các dạng toán và bài tập chuyên đề thứ tự thực hiện phép tính, hỗ trợ giáo viên và học sinh lớp 6 trong quá trình dạy thêm - học thêm môn Toán 6.
PHẦN I. TÓM TẮT LÝ THUYẾT. PHẦN II. CÁC DẠNG BÀI.
Dạng 1. Thực hiện phép tính.
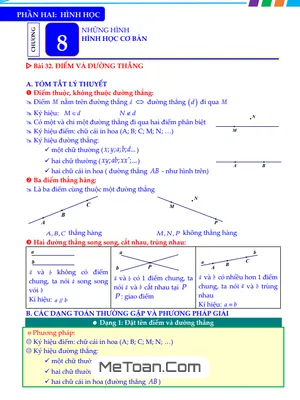
- Đối với biểu thức không chứa dấu ngoặc ta thực hiện phép tính theo thứ tự của chiều mũi tên như sau: Lũy thừa → Nhân – Chia → Cộng – Trừ. Được hiểu là: “Thực hiện nhân chia trước cộng trừ sau”.
- Đối với biểu thức chứa dấu ngoặc, ta thực hiện phép tính trong từng loại ngoặc theo thứ tự của chiều mũi tên như sau: () → [] → {}. Được hiểu là “thực hiện từ trong ra ngoài”.
Dạng 2. Tìm x.
1. Nhắc lại các dạng toán “tìm x” cơ bản.
1.1 Tìm số hạng chưa biết trong một tổng. Muốn tìm số hạng chưa biết trong một tổng, ta lấy tổng trừ đi số hạng đã biết. 1.2 Tìm số bị trừ trong một hiệu. Muốn tìm số bị trừ ta lấy hiệu cộng với số trừ x + a = b => x = b - a. 1.3 Tìm số trừ trong một hiệu. Muốn tìm số trừ ta lấy số bị trừ trừ đi hiệu a - x = b => x = a - b. 1.4 Tìm thừa số chưa biết trong một tích. Muốn tìm thừa số chưa biết trong một tích, ta lấy tích chia cho thừa số đã biết. 1.5 Tìm số bị chia trong một thương. Muốn tìm số bị chia ta lấy thương nhân với số chia x : a = b => x = b * a. 1.6 Tìm số chia trong một thương. Muốn tìm số chia, ta lấy số bị chia chia cho thương a : x = b => x = a : b.
2. Phương pháp giải bài toán “tìm x” ở các dạng mở rộng.
Trong các dạng tìm x mở rộng nào ta cũng phải tìm phần ưu tiên có chứa x (có thể là tìm một lần hoặc tìm nhiều lần) để đưa về dạng cơ bản. Do đó, trong các bài toán “tìm x” ở dạng mở rộng ta phải tìm ra phần ưu tiên trong một bài toán tìm x. 2.1 Dạng ghép. 2.2 Dạng tích. 2.3 Dạng nhiều dấu ngoặc.
3. Phương pháp giải bài toán “tìm x” ở các dạng lũy thừa.
Với dạng toán có lũy thừa, tính lũy thừa trước nếu các lũy thừa không chứa x. Tính ra số tự nhiên hoặc sử dụng các phép toán nhân, chia hai lũy thừa cùng cơ số, tùy vào bài toán cụ thể.
Dạng 3. Các bài toán liên quan đến dãy số, tập hợp.
Tính tổng dãy số: Tổng = (Số đầu + Số cuối) . Số số hạng : 2. Số các số hạng = (Số cuối – Số đầu) : Khoảng cách giữa hai số liên tiếp + 1.
Dạng 4. Bài toán có lời văn.