Phương Pháp Giải Phương Trình Vô Tỷ Hiệu Quả - Trịnh Hồng Uyên

Phương Trình Vô Tỷ - Vấn Đề Quan Trọng Trong Toán Học Phổ Thông

Phương trình vô tỷ là một dạng toán phổ biến và đóng vai trò quan trọng trong chương trình toán học bậc THPT. Nó thường xuất hiện trong các kỳ thi học sinh giỏi và kỳ thi tuyển sinh đại học. Tuy nhiên, học sinh thường gặp khó khăn khi giải quyết các dạng toán này do phương pháp giải chưa được đề cập đầy đủ trong sách giáo khoa. Các phương pháp giải phương trình vô tỷ thường gặp bao gồm đưa về hệ phương trình (đối xứng hoặc không đối xứng), sử dụng phương pháp đặt ẩn phụ không toàn phần, ẩn phụ lượng giác, v.v.

Luận Văn "Một Số Phương Pháp Giải Phương Trình Vô Tỷ" - Hỗ Trợ Giảng Dạy Và Học Tập

Với mong muốn tìm ra những phương pháp giải quyết hiệu quả cho dạng toán này, cũng như tạo ra các phương trình vô tỷ mới, tác giả Trịnh Hồng Uyên đã thực hiện nghiên cứu và cho ra đời luận văn "Một Số Phương Pháp Giải Phương Trình Vô Tỷ". Luận văn này là tài liệu hữu ích, cung cấp cái nhìn tổng quan về phương trình vô tỷ và các phương pháp giải, từ đó hỗ trợ giáo viên trong việc giảng dạy và học sinh trong việc học tập.

Nội Dung Chính Của Luận Văn

Luận văn bao gồm phần mở đầu, ba chương chính, phần kết luận và danh mục tài liệu tham khảo:

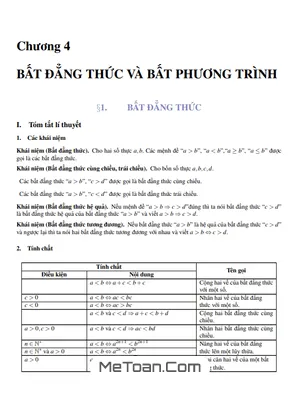
Chương 1: Phương Pháp Giải Phương Trình Vô Tỷ

1.1. Phương pháp hữu tỷ hóa
1.2. Phương pháp ứng dụng các tính chất của hàm số
1.3. Phương pháp đưa về hệ đối xứng
1.4. Phương trình giải bằng phương pháp so sánh

Chương 2: Một Số Phương Pháp Giải Phương Trình Vô Tỷ Chứa Tham Số

2.1. Sử dụng phương pháp biến đổi tương đương
2.2. Sử dụng phương pháp đặt ẩn phụ
2.3. Sử dụng định lí Lagrange
2.4. Sử dụng phương pháp điều kiện cần và đủ
2.5. Sử dụng phương pháp hàm số

Chương 3: Một Số Cách Xây Dựng Phương Trình Vô Tỷ

3.1. Xây dựng phương trình vô tỷ từ các phương trình đã biết cách giải
3.2. Xây dựng phương trình vô tỷ từ hệ phương trình
3.3. Dùng hằng đẳng thức để xây dựng các phương trình vô tỷ
3.4. Xây dựng phương trình vô tỷ dựa theo hàm đơn điệu
3.5. Xây dựng phương trình vô tỷ dựa vào hàm số lượng giác và phương trình lượng giác
3.6. Xây dựng phương trình vô tỷ từ phép đặt ẩn phụ không toàn phần
3.7. Xây dựng phương trình vô tỷ dựa vào tính chất vectơ
3.8. Xây dựng phương trình vô tỷ dựa vào bất đẳng thức
3.9. Xây dựng phương trình vô tỷ bằng phương pháp hình học.

Với nội dung phong phú và được trình bày một cách logic, dễ hiểu, luận văn "Một Số Phương Pháp Giải Phương Trình Vô Tỷ" của tác giả Trịnh Hồng Uyên là tài liệu tham khảo hữu ích cho giáo viên và học sinh trong quá trình giảng dạy và học tập môn Toán.