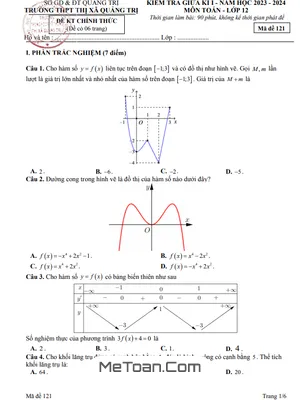
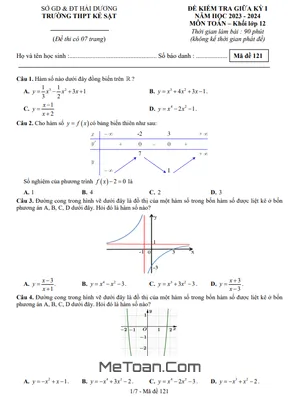
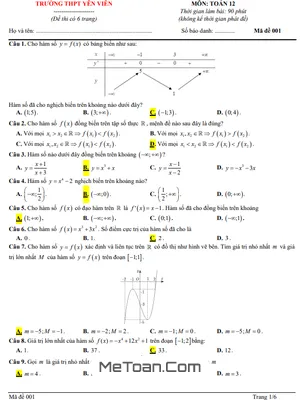
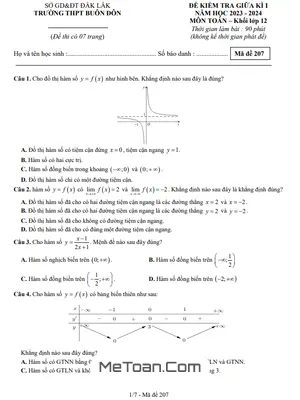
Đề Thi Tham Khảo Giữa HK1 Toán 12 Năm 2020 - 2021 Trường THPT Nguyễn Du - TP HCM

Ôn Tập Hiệu Quả Với Đề Thi Tham Khảo Giữa HK1 Toán 12 Năm 2020 - 2021 Trường THPT Nguyễn Du - TP HCM

Để hỗ trợ các em học sinh lớp 12 trong việc ôn tập và củng cố kiến thức cho kỳ thi giữa học kỳ 1 môn Toán sắp tới, MeToan.Com giới thiệu đến các em đề thi tham khảo giữa HK1 Toán 12 năm 2020 - 2021 trường THPT Nguyễn Du - TP HCM.

Đề thi bao gồm 25 câu trắc nghiệm với thời gian làm bài là 45 phút, đầy đủ đáp án và lời giải chi tiết giúp học sinh tự đánh giá năng lực bản thân.

Trích dẫn một số câu hỏi trong đề thi tham khảo:

Câu 1: Cho hàm số y = f(x) có đạo hàm trên khoảng (a;b). Mệnh đề nào sau đây là sai? A. Nếu f'(x) < 0 với mọi x ∈ (a;b) thì hàm số y = f (x) nghịch biến trên (a;b). B. Nếu f'(x) > 0 với mọi x ∈ (a;b) thì hàm số y = f (x) đồng biến trên (a;b). C. Nếu hàm số y = f (x) nghịch biến trên (a;b) thì f'(x) ≤ 0 với x ∈ (a;b). D. Nếu hàm số y = f (x) đồng biến trên (a;b) thì f'(x) > 0 với x ∈ (a;b).

Câu 2: Cho hàm số f (x) liên tục trên khoảng D ⊂ R và x0 ∈ D. Mệnh đề nào sau đây là đúng? A. x0 là điểm cực đại của hàm số f nếu f (x) > f (x0) với mọi x ∈ D. B. x0 là điểm cực đại của hàm số f nếu với mọi (a;b) ⊂ D chứa x0 ta đều có f (x) > f (x0) với mọi x ∈ (a;b)\ {x0}. C. x0 là cực đại của hàm số f nếu tồn tại (a,b) ⊂ D chứa x0 sao cho f (x) < f (x0) với mọi x ∈ (a;b)\ {x0}. D. x0 là điểm cực đại của hàm số f nếu f (x) < f (x0) với mọi x ∈ (a;b) ⊂ D.

Câu 3: Cho hàm số y = f (x) có bảng biến thiên như sau. Xét các mệnh đề: (I). Hàm số f (x) đồng biến trên khoảng (−∞;2). (II). Hàm số y = f (x) đồng biến trên R. (III). Hàm số không có cực trị. Số các mệnh đề đúng là?

Hy vọng rằng, đề thi tham khảo này sẽ là tài liệu hữu ích giúp các em học sinh lớp 12 ôn tập hiệu quả và tự tin bước vào kỳ thi giữa kỳ 1 môn Toán đạt kết quả cao.