Đề thi học kỳ 1 Toán 12 năm học 2018 - 2019 sở GD&ĐT Nam Định

Chiều thứ Tư, ngày 26 tháng 12 năm 2018, Sở Giáo dục và Đào tạo Nam Định đã tổ chức kỳ thi khảo sát chất lượng học kỳ 1 môn Toán lớp 12 năm học 2018 – 2019. Kỳ thi này nhằm mục đích đánh giá tổng quát kiến thức môn Toán mà học sinh lớp 12 đã được học trong suốt học kỳ 1 vừa qua.

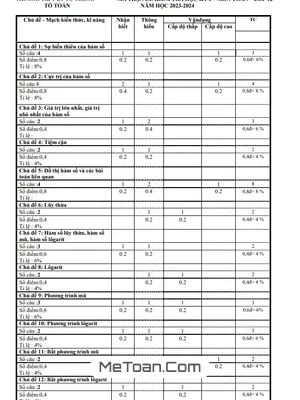
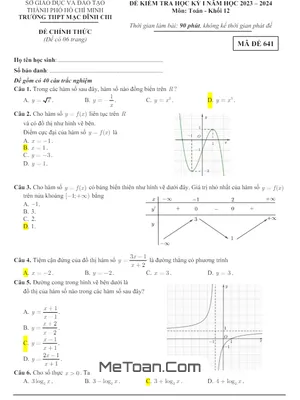
Đề thi được biên soạn theo hình thức trắc nghiệm khách quan với mã đề 132, bao gồm 06 trang với 50 câu hỏi và bài toán. Thí sinh có 90 phút để hoàn thành bài thi. Đây là cấu trúc đề thi quen thuộc, được sử dụng phổ biến ở nhiều trường và sở GD&ĐT trên cả nước. Đề thi có đáp án cho các mã đề 132, 209, 357 và 485.

Dưới đây là một số câu hỏi trích dẫn từ đề thi học kỳ 1 Toán 12 năm học 2018 – 2019 của Sở GD&ĐT Nam Định:

• Câu hỏi về xác suất: Gọi A là tập hợp các số tự nhiên có 4 chữ số khác nhau được tạo ra từ các chữ số 0, 1, 2, 3, 4, 5, 6. Lấy ngẫu nhiên một số từ tập A. Xác suất để số lấy được là số tự nhiên có 4 chữ số khác nhau không lớn hơn 2503 bằng?
• Câu hỏi về ứng dụng đạo hàm: Người ta thiết kế một thùng chứa hình trụ (như hình vẽ) có thể tích V nhất định. Biết rằng giá của vật liệu làm mặt đáy và nắp của thùng bằng nhau và đắt gấp 3 lần so với giá vật liệu để làm mặt xung quanh của thùng (chi phí cho mỗi đơn vị diện tích). Gọi chiều cao của thùng là h và bán kính đáy là r. Tính tỉ số h/r sao cho chi phí vật liệu sản xuất thùng là nhỏ nhất.
• Câu hỏi về hàm số: Cho hàm số y = (3x – 2m)/(mx + 1) với m là tham số. Biết rằng với mọi m khác 0, đồ thị hàm số luôn cắt đường thẳng d: y = 3x – 3m tại hai điểm điểm phân biệt A, B. Tích tất cả các giá trị của tham số m tìm được để đường thẳng d cắt các trục Ox, Oy lần lượt tại C, D sao cho diện tích tam giác OAB bằng 2 lần diện tích tam giác OCD bằng?