Đề thi HK1 Toán 6 năm học 2017 - 2018 phòng GD&ĐT thành phố Ninh Bình

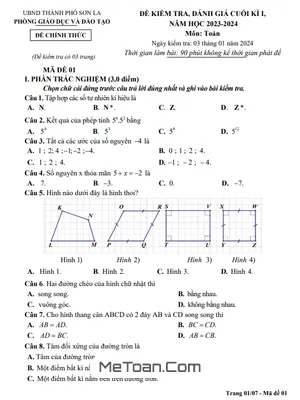
Đề thi học kì 1 môn Toán lớp 6 năm học 2017 - 2018 của phòng GD&ĐT thành phố Ninh Bình gồm 8 câu hỏi trắc nghiệm và 5 bài toán tự luận, thời gian làm bài là 90 phút (không kể thời gian giao đề). Đề thi được biên soạn nhằm mục đích khảo sát chất lượng môn Toán 6 của học sinh trên địa bàn thành phố Ninh Bình.

Dưới đây là trích dẫn một phần của đề thi:

Bài tập: Trên tia Ox vẽ hai điểm M và N sao cho OM = 3 cm, ON = 9 cm.

a) Tính độ dài đoạn thẳng MN?

b) Vẽ điểm A là trung điểm của đoạn thẳng MN. Tính độ dài đoạn thẳng MA?

c) Điểm M có là trung điểm của đoạn thẳng OA hay không? Vì sao?

Lời giải:

a) Trên tia Ox có OM = 3cm; ON = 9 cm. Nên OM < ON (Vì OM=3 cm <ON= 9 cm)

Suy ra điểm M nằm giữa hai điểm O và N.

⇒ OM + MN = ON. Mà OM = 3cm ; ON = 9 cm

⇒ 3 + MN = 9

⇒ MN = 6 (cm)

Vậy MN = 6cm

b) Vì A là trung điểm của đoạn thẳng MN nên:

MA = AN = MN/2 = 6/2 = 3cm

Vậy MA = 3cm

c)Trên tia NO có NO = 9cm; NA = 3 cm nên NA < NO (Vì 3 cm < 9 cm)

Suy ra điểm A nằm giữa hai điểm O và N.

⇒ OA + NA = ON. Mà NA = 3cm; ON = 9 cm

⇒ OA + 3 = 9

⇒ OA = 6 (cm)

Trên tia Ox có OM = 3cm; OA = 6 cm. Nên OM < OA (Vì 3 cm < 6 cm)

Suy ra điểm M nằm giữa hai điểm O và A (1)

Lại có OM = MA (= 3cm) (2)

Từ (1) và (2) suy ra điểm M là trung điểm của đoạn thẳng OA.