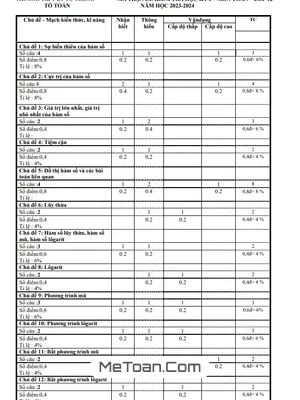
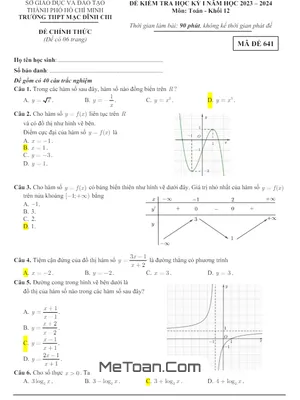
Đề thi HK1 Toán 12 năm 2019 - 2020 trường Nguyễn Khuyến - TP HCM

Trường Nguyễn Khuyến tổ chức kỳ thi học kỳ 1 môn Toán lớp 12 năm học 2019 - 2020

Vào ngày Chủ nhật, 15 tháng 12 năm 2019, trường THCS và THPT Nguyễn Khuyến, thành phố Hồ Chí Minh đã tổ chức kỳ thi kiểm tra cuối học kỳ 1 môn Toán dành cho học sinh lớp 12 năm học 2019 - 2020.

Đề thi HK1 Toán 12 năm học 2019 - 2020 của trường THCS&THPT Nguyễn Khuyến - TP HCM mã đề 485 gồm 04 trang với 30 câu trắc nghiệm và 04 câu tự luận. Tổng thời gian làm bài là 90 phút.

Một số nội dung đáng chú ý trong đề thi:

Hình học không gian: Đề thi yêu cầu học sinh vận dụng kiến thức về hình học không gian để giải quyết các bài toán liên quan đến hình chóp, góc giữa hai mặt phẳng, tính thể tích khối chóp,...
Hình học tọa độ: Phần này tập trung vào việc xác định tọa độ, viết phương trình mặt phẳng, đường thẳng trong không gian.
Ứng dụng đạo hàm: Học sinh cần vận dụng kiến thức về đạo hàm để giải quyết các bài toán liên quan đến tính đơn điệu của hàm số, tìm giá trị lớn nhất, nhỏ nhất của hàm số.

Trích dẫn một số câu hỏi trong đề thi:

Câu hỏi về hình học không gian: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C, BC = 2a. Mặt bên SAB là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa hai mặt phẳng (SAC) và (ABC) bằng 60°. Tính thể tích khối chóp S.ABC.
Câu hỏi về hình học tọa độ: Trong không gian Oxyz, cho mặt cầu (S): (x-1)^2 + (y+2)^2 + (z-3)^2 = 4 và đường thẳng d: (x-2)/1 = (y-1)/-2 = (z+1)/3. Viết phương trình mặt phẳng (P) chứa đường thẳng d và cắt mặt cầu (S) theo một đường tròn có bán kính nhỏ nhất.
Câu hỏi về ứng dụng đạo hàm: Cho hàm số y = f(x) có đạo hàm liên tục trên đoạn [a;b]. Biết rằng f(a) = f(b) = 0 và phương trình f'(x) = 0 có đúng một nghiệm x = c trên khoảng (a;b). Chứng minh rằng hàm số f(x) có giá trị lớn nhất trên đoạn [a;b] bằng 0.