Đề Thi Giữa Kỳ 1 Toán 12 Năm 2025-2026 THPT Nguyễn Công Trứ

Nhằm hỗ trợ quý thầy cô giáo trong công tác giảng dạy và giúp các em học sinh lớp 12 có thêm tài liệu ôn tập chất lượng, MeToan.Com xin giới thiệu bộ đề kiểm tra giữa học kỳ 1 môn Toán năm học 2025 – 2026 của trường THPT Nguyễn Công Trứ, tỉnh Đắk Lắk. Đây là một tài liệu tham khảo giá trị, bám sát cấu trúc chương trình học và giúp học sinh làm quen với các dạng bài thường gặp trước kỳ thi quan trọng.

Nội Dung Trọng Tâm Của Đề Thi

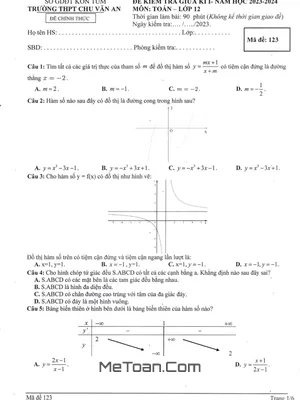
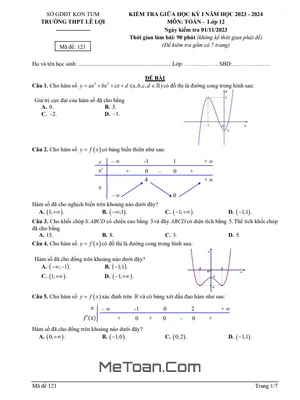
Đề thi tập trung kiểm tra kiến thức trọng tâm của giai đoạn đầu năm học, chủ yếu là Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số. Các câu hỏi trong đề được xây dựng đa dạng, từ mức độ nhận biết, thông hiểu đến vận dụng và vận dụng cao, nhằm đánh giá toàn diện năng lực của học sinh.

Đặc biệt, đề thi có sự xuất hiện của các bài toán ứng dụng thực tế, đòi hỏi học sinh không chỉ nắm vững công cụ đạo hàm mà còn phải có khả năng phân tích và mô hình hóa toán học. Dưới đây là một số câu hỏi tiêu biểu được trích dẫn, thể hiện rõ nét xu hướng ra đề hiện nay:

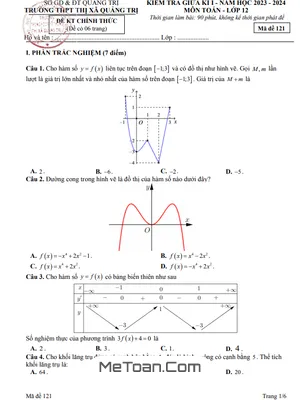
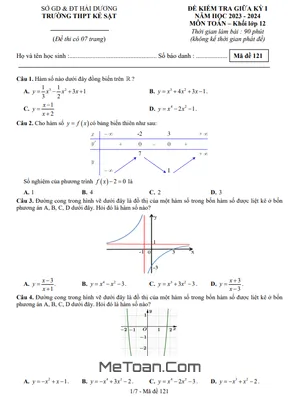
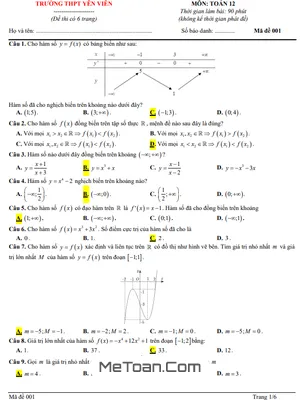
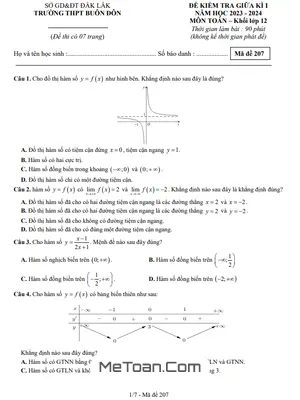
Bài toán tối ưu doanh thu khách sạn: Đây là một dạng toán kinh tế quen thuộc, yêu cầu học sinh thiết lập hàm doanh thu dựa trên mối quan hệ giữa giá phòng và số phòng được thuê. Từ đó, sử dụng đạo hàm để tìm giá trị của biến số (giá phòng) sao cho doanh thu đạt mức cao nhất. Bài toán này không chỉ kiểm tra kiến thức về tìm giá trị lớn nhất của hàm số mà còn rèn luyện tư duy logic và khả năng giải quyết vấn đề thực tiễn.
Bài toán nồng độ thuốc trong máu: Một ví dụ điển hình về ứng dụng của đạo hàm trong lĩnh vực y sinh học. Hàm số biểu diễn nồng độ thuốc đã được cho sẵn, nhiệm vụ của học sinh là tìm thời điểm (biến t) mà tại đó nồng độ thuốc đạt cực đại. Đây là dạng bài kiểm tra trực tiếp kỹ năng khảo sát hàm số để tìm giá trị lớn nhất trên một khoảng xác định.
Bài toán tối ưu thể tích chiếc hộp: Bài toán hình học không gian kết hợp với tối ưu hóa, yêu cầu học sinh từ các kích thước ban đầu của tấm bìa, thiết lập công thức tính thể tích của chiếc hộp theo biến x. Sau đó, tìm giá trị của x trong một đoạn cho trước để thể tích hộp là lớn nhất. Dạng bài này giúp học sinh củng cố kiến thức về cả hình học và giải tích.

Tài Liệu Ôn Tập Hữu Ích

Bộ đề thi được cung cấp kèm theo đáp án chi tiết cho các mã đề 302, 618, 438, 531, giúp các em học sinh có thể tự kiểm tra, đối chiếu kết quả và rút kinh nghiệm sau khi làm bài. Việc luyện tập với các đề thi chính thức từ các trường là một phương pháp hiệu quả để hệ thống hóa kiến thức, rèn luyện kỹ năng làm bài và chuẩn bị tâm lý tốt nhất cho kỳ thi giữa kỳ sắp tới.