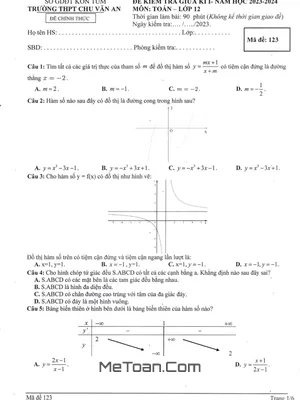
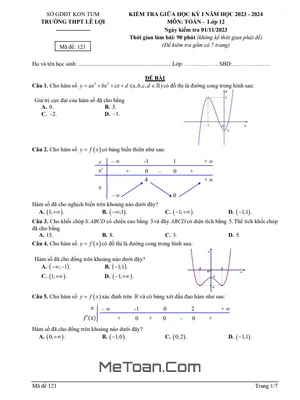
Đề thi giữa kì 1 Toán 12 năm 2025 - 2026 trường THPT Trần Cao Vân, TP.HCM (Có Đáp Án Chi Tiết)

MeToan.Com trân trọng giới thiệu đến quý thầy cô giáo và các em học sinh lớp 12 bộ tài liệu ôn tập chất lượng: đề kiểm tra giữa học kỳ 1 môn Toán năm học 2025 – 2026 của trường THCS & THPT Trần Cao Vân, một trong những trường uy tín tại thành phố Hồ Chí Minh. Đây là tài liệu tham khảo vô cùng hữu ích, giúp các em học sinh làm quen với cấu trúc đề thi mới và củng cố kiến thức một cách hiệu quả trước kỳ thi quan trọng.

Kỳ thi chính thức được tổ chức vào ngày 23 tháng 10 năm 2025, với thời gian làm bài là 90 phút. Cấu trúc đề thi được thiết kế đa dạng nhằm đánh giá toàn diện năng lực của học sinh, bao gồm ba phần chính:

• Phần 1: 12 câu trắc nghiệm nhiều phương án lựa chọn (chiếm 3,0 điểm).
• Phần 2: 04 câu trắc nghiệm dạng Đúng – Sai (chiếm 4,0 điểm).
• Phần 3: 06 câu trắc nghiệm dạng trả lời ngắn (chiếm 3,0 điểm).

Nội dung đề thi bám sát chương trình học, tập trung vào các chuyên đề trọng tâm của nửa đầu học kỳ 1 Toán 12 như: khảo sát sự biến thiên và vẽ đồ thị hàm số, ứng dụng của đạo hàm để tìm giá trị lớn nhất, giá trị nhỏ nhất, và giải quyết các bài toán thực tế. Đặc biệt, tài liệu được cung cấp kèm theo đáp án và lời giải chi tiết cho mã đề gốc, giúp học sinh dễ dàng đối chiếu kết quả và rút kinh nghiệm từ những lỗi sai.

Đề thi nổi bật với các câu hỏi vận dụng và vận dụng cao, đòi hỏi học sinh phải có tư duy logic và khả năng áp dụng kiến thức toán học vào giải quyết các vấn đề thực tiễn. Dưới đây là một số câu hỏi tiêu biểu được trích dẫn từ đề thi:

• Bài toán tối ưu lợi nhuận: Một doanh nghiệp sản xuất x sản phẩm trong một tháng (x thuộc N*; 1 ≤ x ≤ 7000). Chi phí sản xuất bình quân cho mỗi sản phẩm (đơn vị: nghìn đồng) được cho bởi hàm G(x) = 2x + 270. Người ta xây dựng hàm doanh thu (đơn vị: nghìn đồng) của doanh nghiệp theo công thức F(x) = x³ – 20487x² + 139929570x – 318539780000. Giả sử toàn bộ sản phẩm sản xuất ra đều được tiêu thụ. Hỏi doanh nghiệp cần sản xuất ít nhất bao nhiêu sản phẩm để lợi nhuận thu được ≥ 100 triệu đồng?

• Bài toán ứng dụng đạo hàm: Giả sử độ giảm đau của một bệnh nhân khi dùng một loại thuốc được mô tả bởi hàm R(x) = x²(60 – x) với 0 ≤ x ≤ 60, trong đó x là liều lượng thuốc (đơn vị: mg). Hỏi nên tiêm cho bệnh nhân liều lượng thuốc bao nhiêu để độ giảm đau đạt giá trị lớn nhất?.

• Bài toán hình học không gian Oxyz: Trong không gian Oxyz, cho tam giác ABC có tọa độ A(507;525;502), B(500;501;502), C(520;516;502). Tính độ dài HK với H là tọa độ chân đường cao hạ từ đỉnh A xuống cạnh BC, K là tọa độ chân đường phân giác trong của góc B, (K thuộc AC) (không làm tròn kết quả các phép tính trung gian, chỉ làm tròn kết quả cuối cùng đến hàng phần mười).

Việc luyện tập với đề thi này không chỉ giúp các em học sinh hệ thống hóa kiến thức mà còn là cơ hội để rèn luyện kỹ năng quản lý thời gian và chiến thuật làm bài hiệu quả. Chúc các em đạt kết quả cao trong kỳ thi sắp tới!