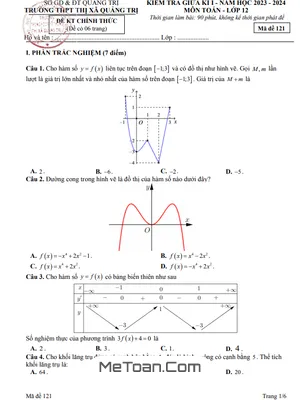
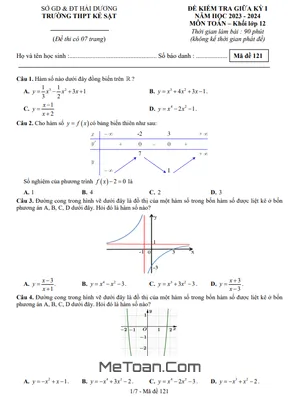
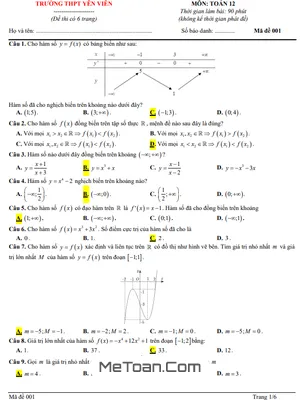
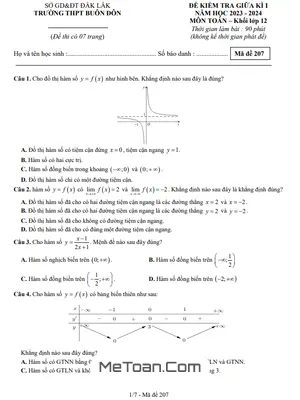
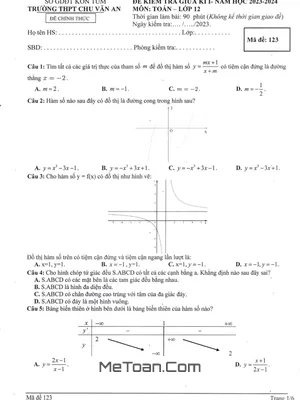
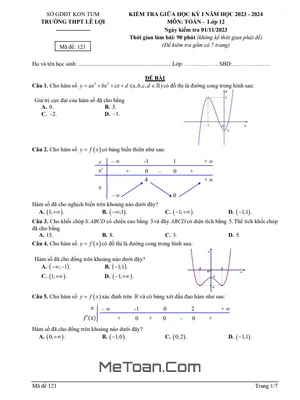
Đề Thi Giữa Kì 1 Toán 12 Năm 2024 - 2025 Trường THPT Yên Lạc - Vĩnh Phúc

Đề Thi Giữa Kì 1 Toán 12 Năm 2024 - 2025 Trường THPT Yên Lạc - Vĩnh Phúc
MeToan.Com trân trọng giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra giữa học kì 1 môn Toán 12 năm học 2024 – 2025 trường THPT Yên Lạc, tỉnh Vĩnh Phúc. Đề thi được biên soạn theo hình thức trắc nghiệm mới nhất, với cấu trúc gồm 03 phần: trắc nghiệm 04 lựa chọn, trắc nghiệm đúng sai, trả lời ngắn; thời gian làm bài 90 phút, có đáp án mã đề 101 102 103 104.
Trích dẫn Đề giữa kì 1 Toán 12 năm 2024 – 2025 trường THPT Yên Lạc – Vĩnh Phúc:
Bài toán thực tế về sản xuất vải lụa: Một hộ gia đình làm nghề dệt vải lụa tơ tằm sản xuất mỗi ngày được x mét vải lụa (với điều kiện 1 ≤ x ≤ 18). Tổng chi phí để sản xuất x mét vải lụa, tính bằng đơn vị nghìn đồng, được cho bởi hàm chi phí C(x) = x³ – 3x² – 20x + 500. Giả sử hộ làm nghề dệt này bán hết sản phẩm mỗi ngày với giá 220 nghìn đồng / mét. Gọi B(x) là số tiền bán được và L(x) là lợi nhuận thu được khi bán x mét vải lụa.
Bài toán tối ưu hóa trong xây dựng: Một khu chung cư muốn xây dựng một bể chứa nước có dạng một khối hình hộp chữ nhật có nắp đậy, có thể tích bằng 576 m³. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng. Chi phí vật liệu xây dựng và thuê công nhân để xây bể là 500.000 đồng / m². Yêu cầu tính chi phí thấp nhất (tính theo đơn vị triệu đồng) để xây dựng bể chứa nước này.
Bài toán ứng dụng đạo hàm trong kinh doanh: Một nhà sản xuất trung bình bán được 1000 ti vi mỗi tuần với giá 14 triệu đồng một chiếc. Một cuộc khảo sát thị trường chỉ ra rằng nếu cứ giảm giá bán 500 nghìn đồng, số lượng ti vi bán ra sẽ tăng 100 ti vi mỗi tuần. Biết hàm chi phí hàng tuần là C(x) = 12000 – 3x (triệu đồng), trong đó x là số ti vi bán ra ở mỗi tuần. Yêu cầu xác định giá bán (triệu đồng) mà nhà sản xuất nên đặt để lợi nhuận đạt lớn nhất.