Đề Cương Ôn Tập Giữa Kỳ 1 Toán 12 Năm 2023 - 2024 Trường Bùi Thị Xuân - Lâm Đồng

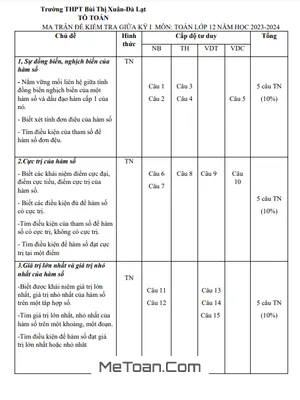
Đề Cương Ôn Tập Giữa Kỳ 1 Môn Toán 12 Năm Học 2023 - 2024 - Trường THPT Bùi Thị Xuân - Lâm Đồng

MeToan.Com trân trọng giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề cương ôn tập giữa học kỳ 1 môn Toán 12 năm học 2023 – 2024 trường THPT Bùi Thị Xuân, thành phố Đà Lạt, tỉnh Lâm Đồng.

GIẢI TÍCH

1. Sự Đồng Biến, Nghịch Biến Của Hàm Số

• Nắm vững mối liên hệ giữa tính đồng biến nghịch biến của một hàm số và dấu đạo hàm cấp một của nó.
• Biết xét tính đơn điệu của hàm số.
• Tìm điều kiện của tham số để hàm số đơn điệu.

2. Cực Trị Của Hàm Số

• Biết các khái niệm điểm cực đại, điểm cực tiểu, điểm cực trị của hàm số.
• Biết các điều kiện đủ để hàm số có cực trị.
• Tìm điều kiện của tham số để hàm số có cực trị, không có cực trị.
• Tìm điều kiện để hàm số đạt cực trị tại một điểm.

3. Giá Trị Lớn Nhất Và Giá Trị Nhỏ Nhất Của Hàm Số

• Biết được khái niệm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một tập hợp số.
• Tìm giá trị lớn nhất, nhỏ nhất của hàm số trên một khoảng, một đoạn.
• Tìm điều kiện để hàm số đạt giá trị lớn nhất hoặc nhỏ nhất.

4. Đường Tiệm Cận

• Khái niệm đường tiệm cận đứng, tiệm cận ngang của đồ thị hàm số.
• Tìm tiệm cận đứng, tiệm cận ngang của đồ thị hàm số.

5. Khảo Sát Sự Biến Thiên Và Vẽ Đồ Thị Hàm Số

• Nhận dạng đồ thị hàm số bậc ba, bậc bốn trùng phương, phân thức hữu tỉ bậc nhất / bậc nhất.
• Vận dụng đồ thị để giải các bài toán liên quan.

HÌNH HỌC

1. Khái Niệm Về Khối Đa Diện. Khối Đa Diện Lồi - Đều

• Nhận biết được các khối đa diện, biết cách phân chia một khối đa diện thành các khối đa diện nhỏ hơn.
• Nhận biết được các khối đa diện. So sánh được khối đa diện bằng nhau.
• Hình dung trực quan về năm loại khối đa diện đều.

2. Tính Góc - Tính Khoảng Cách

• Nắm chắc phương pháp tính góc giữa đường thẳng và mặt phẳng, góc giữa mặt phẳng và mặt phẳng.
• Tính được khoảng cách từ một điểm đến mặt phẳng. Khoảng cách giữa hai đường thẳng chéo nhau.

3. Thể Tích Khối Chóp. Thể Tích Khối Lăng Trụ

• Tính được thể tích khối chóp và khối lăng trụ.