Áp dụng Kỹ Thuật Truy Hàm Hiện Đại để Tính Diện Tích Hình Phẳng Chính Xác
Tài liệu chuyên sâu, dày 30 trang, được biên soạn tỉ mỉ bởi tác giả Anh Shiper Toán, mang đến một góc nhìn toàn diện về việc khai thác kỹ thuật truy hàm để xác định diện tích các khu vực hình phẳng phức tạp. Đây là một phương pháp then chốt, đặc biệt hữu ích trong các bài toán hình học giải tích nâng cao và là công cụ đắc lực cho các kỳ thi cạnh tranh. Việc làm chủ phương pháp này giúp người học tiếp cận các bài toán khó một cách hệ thống và hiệu quả hơn.
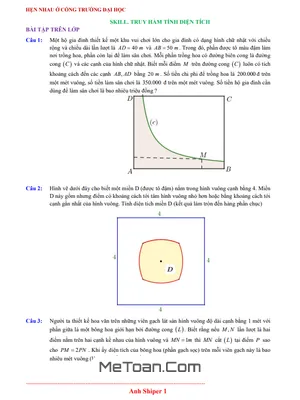
Nội dung tài liệu đi sâu vào cách thức áp dụng phương pháp này thông qua hàng loạt ví dụ thực tế và đa dạng. Một trong số đó là bài toán thiết kế khu vui chơi gia đình hình chữ nhật, trong đó khu vực trồng hoa được giới hạn bởi một đường cong độc đáo. Đường cong này được định nghĩa dựa trên tích khoảng cách của mỗi điểm đến hai cạnh kề, tạo ra một thách thức tính toán diện tích cụ thể của cả khu vực trồng hoa lẫn sân chơi, từ đó suy ra tổng chi phí. Bài toán này không chỉ yêu cầu kiến thức vững về tích phân mà còn đòi hỏi sự tinh tế trong việc thiết lập hệ tọa độ và biểu diễn hàm số một cách khéo léo để tối ưu hóa quá trình tính toán.
Một ví dụ hấp dẫn khác khám phá thiết kế hoa văn trên gạch lát sàn. Bông hoa trung tâm trên viên gạch hình vuông được bao quanh bởi một đường cong (L), mà định nghĩa của nó lại phụ thuộc vào tỷ lệ đoạn thẳng (PM = 2PN) khi một đoạn thẳng MN nối hai cạnh kề của viên gạch. Tình huống này đòi hỏi người học phải có khả năng chuyển đổi các điều kiện hình học phức tạp thành phương trình hàm số rõ ràng để tiến hành tính toán diện tích một cách chính xác, thể hiện sự linh hoạt của kỹ thuật truy hàm trong việc giải quyết các bài toán hình học không gian phẳng.
Ngoài ra, tài liệu còn đề cập đến các mẫu hoa văn trên gạch lát nền được tạo hình từ nhiều đường cong đối xứng, ví dụ như đường (L1) được định nghĩa qua mối quan hệ khoảng cách (MA = √2d(M;Δ)) và đường (L2) đối xứng qua trục Ox. Những bài toán này không chỉ yêu cầu tính toán từng phần diện tích riêng lẻ mà còn tổng hợp chúng, mang đến một cái nhìn tổng quan về việc áp dụng linh hoạt phương pháp truy hàm trong các tình huống hình học đa dạng và phức tạp, từ đó phát triển kỹ năng tư duy và giải quyết vấn đề.
Với các hướng dẫn chi tiết và ví dụ minh họa phong phú, tài liệu này không chỉ cung cấp các lời giải cụ thể mà còn trang bị cho người đọc tư duy phân tích và kỹ năng giải quyết các bài toán về diện tích hình phẳng tưởng chừng khó khăn. Đây là một nguồn tài liệu giá trị, không thể thiếu cho những ai muốn nâng cao năng lực trong lĩnh vực hình học giải tích và ứng dụng toán học vào thực tiễn.























