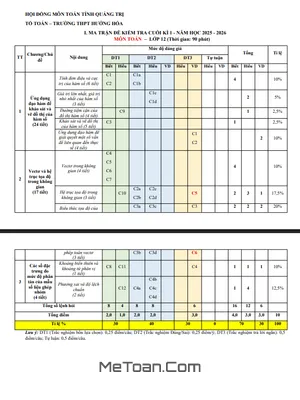
Đề cương Ôn Tập Cuối Kì 1 Môn Toán 12 Năm Học 2025 – 2026 Trường THPT Hướng Hóa

MeToan.Com hân hạnh giới thiệu đến quý thầy, cô giáo cùng toàn thể các em học sinh một tài liệu vô cùng giá trị: đề cương ôn tập kiểm tra cuối học kì 1 môn Toán lớp 12, áp dụng cho năm học 2025 – 2026 của Trường THPT Hướng Hóa, tỉnh Quảng Trị. Tài liệu này được biên soạn kỹ lưỡng nhằm cung cấp một lộ trình ôn luyện rõ ràng, giúp các em hệ thống hóa kiến thức trọng tâm và tự tin bước vào kì thi sắp tới.

Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số (24 tiết)

Phần đầu tiên và cũng là một trong những chuyên đề cốt lõi của chương trình Toán 12 là 'Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số', kéo dài 24 tiết. Chuyên đề này trang bị cho học sinh những công cụ mạnh mẽ để phân tích sâu sắc các đặc tính của hàm số, từ đó hiểu rõ hơn về hành vi và hình dạng của chúng.

Tính đơn điệu và cực trị của hàm số (6 tiết): Các em sẽ được học cách xác định khoảng đồng biến, nghịch biến của hàm số, tìm các điểm cực đại, cực tiểu – những điểm quan trọng thể hiện sự thay đổi xu hướng của đồ thị. Đây là nền tảng vững chắc để hiểu cấu trúc cơ bản của hàm số.
Giá trị lớn nhất, giá trị nhỏ nhất của hàm số (3 tiết): Chuyên đề này tập trung vào việc tìm kiếm các giá trị cực biên của hàm số trên một đoạn hoặc khoảng xác định, có nhiều ứng dụng trong tối ưu hóa các bài toán thực tế.
Đường tiệm cận của đồ thị hàm số (4 tiết): Học sinh sẽ nghiên cứu về tiệm cận đứng, tiệm cận ngang và tiệm cận xiên, giúp phác thảo chính xác hình dạng của đồ thị khi biến số tiến ra vô cùng hoặc gần đến một giá trị cụ thể.
Khảo sát và vẽ đồ thị của hàm số (5 tiết): Đây là tổng hợp của các kiến thức trên, giúp các em thực hiện một quy trình hoàn chỉnh từ việc lập bảng biến thiên, tìm tiệm cận, tính các điểm đặc biệt để từ đó vẽ được đồ thị hàm số một cách chính xác.
Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tế (4 tiết): Đặc biệt, các em sẽ được tiếp cận với những bài toán thực tiễn phong phú, từ kinh tế, kỹ thuật đến vật lý, nơi đạo hàm trở thành công cụ đắc lực để giải quyết các vấn đề tối ưu hóa lợi nhuận, tìm vận tốc tức thời, hay xác định các điều kiện tối ưu khác.

Vectơ và hệ trục tọa độ trong không gian (17 tiết)

Phần thứ hai chuyển sang lĩnh vực hình học không gian với chuyên đề 'Vectơ và hệ trục tọa độ trong không gian', tổng cộng 17 tiết. Chuyên đề này mở rộng tư duy hình học của học sinh từ mặt phẳng lên không gian ba chiều, là tiền đề cho việc học về mặt phẳng, đường thẳng và các khối đa diện trong không gian.

Vectơ trong không gian (4 tiết): Các em sẽ được làm quen với khái niệm vectơ trong không gian, các phép toán cơ bản như cộng, trừ vectơ, nhân vectơ với một số, và tích vô hướng của hai vectơ.
Hệ trục tọa độ trong không gian (3 tiết): Đây là phần giới thiệu về hệ trục tọa độ Descartes Oxyz, giúp biến các bài toán hình học thành các bài toán đại số thông qua tọa độ điểm và tọa độ vectơ, mở ra một phương pháp giải mới.
Biểu thức tọa độ của phép toán vectơ (3 tiết): Học sinh sẽ học cách thực hiện các phép toán vectơ bằng tọa độ, tính khoảng cách giữa hai điểm, tọa độ trung điểm, và các công thức liên quan khác, làm nền tảng cho việc giải quyết các bài toán hình học giải tích phức tạp hơn.

Các số đặc trưng đo mức độ phân tán của mẫu số liệu ghép nhóm (4 tiết)

Cuối cùng, đề cương đề cập đến một chuyên đề quan trọng trong thống kê: 'Các số đặc trưng đo mức độ phân tán của mẫu số liệu ghép nhóm', gói gọn trong 4 tiết. Chuyên đề này giúp các em hiểu rõ hơn về sự biến động, phân tán của dữ liệu chứ không chỉ dừng lại ở các số đo trung tâm.

Khoảng biến thiên và khoảng tứ phân vị (1 tiết): Học sinh sẽ học cách xác định phạm vi biến thiên của dữ liệu và hiểu về khoảng tứ phân vị (IQR), cung cấp cái nhìn về sự phân bố của 50% dữ liệu ở giữa, giúp đánh giá sự đồng nhất của mẫu số liệu.
Phương sai và độ lệch chuẩn (2 tiết): Hai khái niệm này là những số đo quan trọng nhất để đánh giá mức độ phân tán của các giá trị trong một tập dữ liệu so với giá trị trung bình. Việc nắm vững phương sai và độ lệch chuẩn giúp phân tích dữ liệu một cách sâu sắc và đưa ra những nhận định chính xác về độ ổn định của dữ liệu.

Đề cương này không chỉ là danh sách các chủ đề mà còn là bản đồ dẫn lối, giúp các em định hướng ôn tập hiệu quả và tập trung vào những kiến thức trọng yếu. MeToan.Com hy vọng rằng với sự chuẩn bị chu đáo và tinh thần học hỏi, tất cả các em học sinh Trường THPT Hướng Hóa sẽ đạt được kết quả cao nhất trong kì thi cuối học kì 1 sắp tới. Chúc các em ôn tập thành công và gặt hái nhiều thành tích xuất sắc!