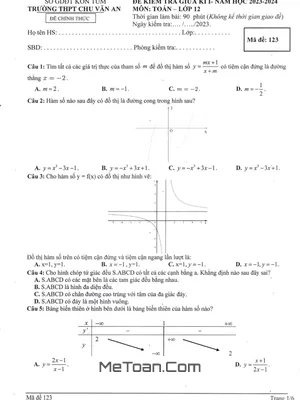
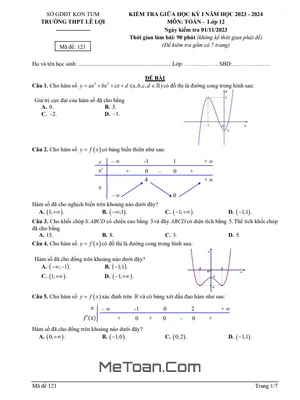
Đề thi Giữa Học Kì 1 Toán 12 năm 2025 – 2026 trường Trưng Vương

MeToan.Com xin trân trọng giới thiệu đến quý thầy cô giáo và các em học sinh lớp 12 bộ đề kiểm tra giữa học kì 1 môn Toán năm học 2025 – 2026 của trường THCS và THPT Trưng Vương, tỉnh Vĩnh Long. Đây là một tài liệu tham khảo hữu ích, giúp các em học sinh củng cố kiến thức đã học, rèn luyện kỹ năng giải toán và chuẩn bị tốt nhất cho kỳ thi sắp tới.

Cấu trúc chi tiết của đề thi

Đề thi được thiết kế theo định dạng mới nhằm đánh giá toàn diện kiến thức và năng lực của học sinh. Cấu trúc đề bao gồm 3 phần chính với các hình thức câu hỏi đa dạng:

Trắc nghiệm nhiều phương án lựa chọn: Phần này gồm các câu hỏi trắc nghiệm khách quan, mỗi câu trả lời đúng được 0,25 điểm. Đây là phần kiểm tra kiến thức nền tảng và tốc độ xử lý bài toán của học sinh.
Trắc nghiệm Đúng - Sai: Đây là dạng câu hỏi mới, yêu cầu học sinh phải phân tích kỹ từng nhận định để đưa ra lựa chọn chính xác. Điểm tối đa cho mỗi câu hỏi ở phần này là 1 điểm, đánh giá khả năng hiểu sâu vấn đề.
Trắc nghiệm trả lời ngắn: Ở phần này, học sinh cần tự tìm ra kết quả cuối cùng và điền vào phiếu trả lời. Mỗi câu trả lời đúng được 0,5 điểm, đòi hỏi kỹ năng tính toán chính xác và cẩn thận.

Nội dung ôn tập trọng tâm

Nội dung kiến thức trong đề thi tập trung chủ yếu vào chương đầu tiên của chương trình Giải tích 12: "Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số". Các chủ đề chính bao gồm:

Sự đồng biến, nghịch biến và cực trị của hàm số: Nắm vững cách xét dấu đạo hàm y' để tìm các khoảng đơn điệu và xác định các điểm cực đại, cực tiểu của hàm số.
Giá trị lớn nhất và giá trị nhỏ nhất (GTLN - GTNN): Rèn luyện kỹ năng tìm GTLN, GTNN của một hàm số trên một đoạn, một khoảng hoặc trên tập xác định.
Đường tiệm cận: Hiểu rõ và tìm được các đường tiệm cận đứng, tiệm cận ngang của đồ thị hàm số, đặc biệt là các hàm phân thức hữu tỉ.
Khảo sát và vẽ đồ thị hàm số: Thực hiện thành thạo các bước khảo sát sự biến thiên và vẽ đồ thị của các hàm số quen thuộc như hàm bậc ba, hàm bậc bốn trùng phương.
Ứng dụng đạo hàm vào bài toán thực tiễn: Vận dụng kiến thức về đạo hàm để giải quyết các bài toán tối ưu hóa trong thực tế như tìm lợi nhuận lớn nhất, chi phí nhỏ nhất, hoặc các bài toán liên quan đến chuyển động.

Chúc các em học sinh ôn tập hiệu quả và đạt được kết quả cao trong kỳ thi giữa học kỳ 1 sắp tới!