Đề Thi Giữa Kỳ 1 Toán 9 Năm Học 2025 - 2026 Trường THCS Lưu Văn Lang, Đồng Tháp (Kèm Đáp Án Chi Tiết)

Để hỗ trợ quý thầy, cô giáo trong công tác giảng dạy và giúp các em học sinh lớp 9 có thêm tài liệu ôn tập chất lượng, MeToan.Com xin giới thiệu bộ đề kiểm tra giữa học kỳ 1 môn Toán năm học 2025 – 2026. Đây là đề thi chính thức của trường THCS Lưu Văn Lang, thuộc phường Sa Đéc, tỉnh Đồng Tháp, được tổ chức vào tháng 11 năm 2025. Bộ tài liệu đi kèm đáp án và thang điểm chi tiết, là nguồn tham khảo đáng tin cậy để học sinh tự đánh giá kiến thức và chuẩn bị tốt nhất cho kỳ thi.
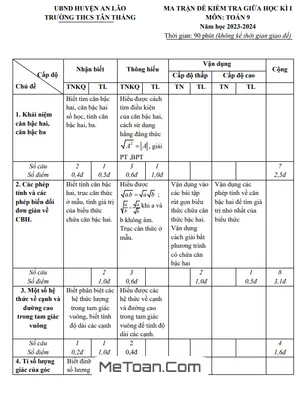
Đề thi được xây dựng dựa trên một ma trận kiến thức rõ ràng, bám sát chương trình học, giúp học sinh hệ thống hóa các nội dung trọng tâm đã học trong nửa đầu năm học. Cấu trúc kiến thức của đề thi được phân bổ cụ thể như sau:
1. Chủ đề về Phương trình và Hệ phương trình (15 tiết) Đây là chuyên đề quan trọng, chiếm tỷ trọng lớn trong đề thi. Nội dung bao gồm hai phần chính:
- Phương trình quy về phương trình bậc nhất một ẩn (4 tiết): Học sinh cần nắm vững các kỹ năng biến đổi, giải các dạng phương trình cơ bản, phương trình chứa ẩn ở mẫu và các bài toán thực tế liên quan.
- Phương trình và hệ phương trình bậc nhất hai ẩn (11 tiết): Trọng tâm của phần này là kỹ năng giải hệ phương trình bằng các phương pháp thế, cộng đại số và đặt ẩn phụ. Bên cạnh đó, các bài toán ứng dụng giải bằng cách lập hệ phương trình cũng là một phần không thể thiếu.
2. Chủ đề về Lượng giác và Hệ thức trong tam giác vuông (10 tiết) Phần kiến thức hình học này yêu cầu học sinh vận dụng linh hoạt các công thức và định lý. Nội dung tập trung vào:
- Tỉ số lượng giác của góc nhọn: Nắm vững định nghĩa các tỉ số sin, cos, tan, cot và mối quan hệ giữa chúng.
- Hệ thức về cạnh và góc trong tam giác vuông: Vận dụng các định lý Pytago, các hệ thức lượng để giải tam giác vuông và giải quyết các bài toán hình học có liên quan.
3. Chủ đề về Bất đẳng thức và Bất phương trình (8 tiết) Chuyên đề này giúp phát triển tư duy logic và kỹ năng chứng minh cho học sinh. Các kiến thức cốt lõi bao gồm:
- Bất đẳng thức: Hiểu và áp dụng các tính chất cơ bản của bất đẳng thức để so sánh và chứng minh.
- Bất phương trình bậc nhất một ẩn: Nắm vững quy tắc biến đổi, cách giải và biểu diễn tập nghiệm của bất phương trình trên trục số.