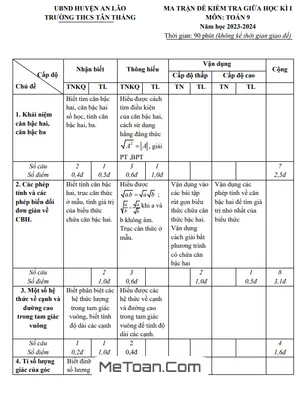
Đề Thi Giữa Học Kỳ 1 Môn Toán Lớp 9 (2025–2026)

MeToan.Com vừa giới thiệu đến quý thầy, cô giáo và các em học sinh một tài liệu ôn tập cực kỳ quan trọng: đề kiểm tra đánh giá chất lượng giữa học kỳ 1 môn Toán lớp 9, áp dụng cho năm học 2025 – 2026. Đề thi này được biên soạn bởi Trường Trung học Cơ sở An Lão, thuộc xã Bình Sơn, tỉnh Ninh Bình, là nguồn tư liệu tham khảo hữu ích giúp học sinh nắm vững cấu trúc đề và các dạng bài trọng tâm.

Cấu Trúc Đề Thi và Thời Gian Làm Bài

Đề kiểm tra giữa kỳ 1 Toán 9 của trường THCS An Lão được xây dựng theo hình thức chuẩn của Bộ Giáo dục và Đào tạo, kết hợp hài hòa giữa kiến thức cơ bản và nâng cao. Cấu trúc đề bao gồm 20% câu hỏi trắc nghiệm khách quan, kiểm tra nhanh các khái niệm và định lý cơ bản, và 80% bài toán tự luận, đòi hỏi kỹ năng trình bày, giải quyết vấn đề chi tiết. Tổng thời gian hoàn thành bài kiểm tra là 90 phút, yêu cầu học sinh phải có sự phân bổ thời gian hợp lý.

Phân Tích Các Dạng Bài Tự Luận Trọng Tâm

Phần tự luận chiếm tỷ trọng lớn nhất, tập trung vào các chuyên đề quan trọng của chương trình Toán 9 nửa đầu năm học:

1. Bài Toán Giải Hệ Phương Trình (Bài toán về năng suất):

Đây là dạng toán kinh điển đòi hỏi học sinh phải thiết lập được hệ phương trình bậc nhất hai ẩn từ các dữ kiện cho trước. Bài toán cụ thể yêu cầu tính thời gian hoàn thành công việc độc lập của hai người thợ. Dữ liệu phức tạp nằm ở việc phải xử lý đơn vị thời gian (4 giờ 30 phút) và tỷ lệ công việc (50%) để xây dựng mối quan hệ giữa năng suất của mỗi người. Việc giải chính xác hệ phương trình sẽ quyết định đáp án cuối cùng.

2. Hình Học và Hệ Thức Lượng trong Tam Giác Vuông:

Chuyên đề hình học tập trung vào việc áp dụng các hệ thức lượng trong tam giác vuông và đường cao. Với $\triangle ABC$ vuông tại $A$, đường cao $AH$, các yêu cầu tính toán cơ bản như tính $AH, AB, AC$ dựa trên độ dài $BH = 4cm$ và $HC = 6cm$ là bắt buộc. Ngoài ra, bài toán nâng cao hơn yêu cầu chứng minh sự đồng dạng của hai tam giác: $\triangle BKC$ và $\triangle BHM$, sau khi xác định trung điểm $M$ của $AC$ và kẻ $AK \perp BM$. Đây là phần thử thách kỹ năng vận dụng định lý và tư duy hình học của học sinh.

3. Ứng Dụng Thực Tế của Tỉ Số Lượng Giác (Độ Dốc):

Bài toán thực tế về quãng đường leo dốc là một ứng dụng tiêu biểu của lượng giác. Học sinh phải sử dụng các tỉ số lượng giác (sin, cos, tan) để tính quãng đường đi ($AC$ và $CB$) dựa vào chiều cao $12m$ và các góc nghiêng ($6^\circ$ khi lên dốc, $4^\circ$ khi xuống dốc). Đặc biệt, học sinh cần chuyển đổi đơn vị tốc độ (km/h) và quãng đường (mét) một cách linh hoạt, sau đó tính tổng thời gian đi từ $A$ đến $B$, yêu cầu làm tròn kết quả đến hàng đơn vị (quãng đường) và phút (thời gian). Đây là bài toán tổng hợp kiểm tra khả năng áp dụng kiến thức Toán vào đời sống một cách chính xác.