Đề thi học kỳ 1 Toán 7 năm học 2017 - 2018 trường THCS Nguyễn Trãi - Đắk Lắk
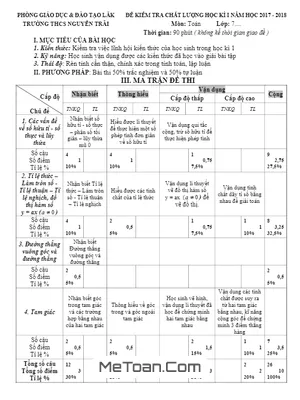
Đề thi học kỳ 1 môn Toán lớp 7 năm học 2017 - 2018 của trường THCS Nguyễn Trãi (tỉnh Đắk Lắk) được biên soạn theo hình thức tự luận với 20 câu hỏi trắc nghiệm và 3 bài toán tự luận. Thời gian làm bài là 90 phút. Đề thi có kèm theo đáp án và lời giải chi tiết cho từng câu hỏi, giúp học sinh tham khảo và ôn tập hiệu quả.
Dưới đây là một phần của đề thi:
Bài tập: Cho tam giác ABC vuông tại A biết AB < AC. Trên đoạn thẳng AC lấy điểm D sao cho AB = AD, trên tia đối của tia BA lấy điểm E sao cho AE = AC. Gọi I là giao điểm của ED và BC.
a/ Vẽ hình và ghi giả thiết kết luận của bài toán
b/ Chứng minh rằng: hai tam giác EIB và CID bằng nhau
c/ Gọi H là trung điểm của đoạn thẳng EC. Chứng minh rằng: Ba điểm A; I; H thẳng hàng
Lời giải:
a) Giả thiết:
- Tam giác ABC vuông tại A
- AB = AD
- AE = AC
- HE = HC
Kết luận:
- Hai tam giác EIB và CID bằng nhau
- Ba điểm A, I, H thẳng hàng
b) Xét tam giác CAB và tam giác EAD có:
- CA = EA (Theo giả thiết)
- Góc A chung
- BA = DA
Suy ra hai tam giác CAB và EAD bằng nhau (c.g.c), suy ra hai góc AED và ACB bằng nhau.
Ta có: AE = AC, AB = AD suy ra AE – AB = AC – AD, suy ra BE = CD
c) Xét tam giác EIH và tam giác CIH có:
- IE = IC (do tam giác EIB = tam giác CID)
- IH chung
- HE = HC (Theo giả thiết)
Suy ra tam giác EIH và tam giác CIH bằng nhau (c.c.c)
Suy ra góc EHI và góc CHI bằng nhau
Mà góc EHI + góc CHI = 180 độ. Suy ra góc EHI = 90 độ, suy ra IH vuông góc với EC (1)
Xét tam giác AEH và tam giác ACH có:
- AE = AC
- AH chung
- HE = HC
Suy ra hai tam giác AEH và ACH bằng nhau (c.c.c)
Suy ra góc AHE và AHC bằng nhau, mà AHE + AHC = 180 độ, do đó AHE = 90 độ
Vậy AH ⊥ EC (2)
Từ (1) và (2) suy ra: A; I; H thẳng hàng.























