Bài Tập Tự Luận Chuyên Đề Vectơ - Trần Đình Thiên

Tài liệu gồm 18 trang tóm tắt lý thuyết, phân loại các dạng toán và tổng hợp các bài toán tự luận chủ đề vectơ, tích vô hướng của hai vectơ và ứng dụng.

Chương 1. Vectơ

I. Vectơ

Vấn đề 1. Khái niệm vectơ
Vấn đề 2. Chứng minh đẳng thức vectơ – phân tích vectơ

Để chứng minh một đẳng thức vectơ hoặc phân tích một vectơ theo hai vectơ không cùng phương, ta thường sử dụng:

Qui tắc ba điểm để phân tích các vectơ
Các hệ thức thường dùng như: Hệ thức trung điểm, hệ thức trọng tâm tam giác
Tính chất của các hình
Vấn đề 3. Xác định một điểm thoả mãn đẳng thức vectơ

Để xác định một điểm M ta cần phải chỉ rõ vị trí của điểm đó đối với hình vẽ. Thông thường ta biến đổi đẳng thức vectơ đã cho về dạng $\overrightarrow{OM}$ = $\overrightarrow{a}$, trong đó O và $\overrightarrow{a}$ đã được xác định. Ta thường sử dụng các tính chất về:

Điểm chia đoạn thẳng theo tỉ số k
Hình bình hành
Trung điểm của đoạn thẳng
Vấn đề 4. Chứng minh ba điểm thẳng hàng – hai điểm trùng nhau

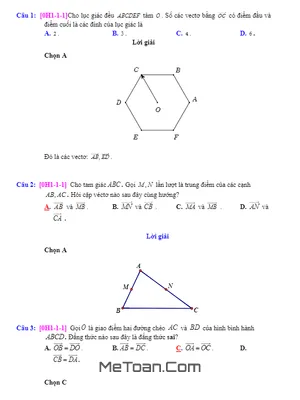
Để chứng minh ba điểm A, B, C thẳng hàng ta chứng minh ba điểm đó thoả mãn đẳng thức $\overrightarrow{AB}$ = k.$\overrightarrow{AC}$, với k khác 0 Để chứng minh hai điểm M, N trùng nhau ta chứng minh chúng thoả mãn đẳng thức $\overrightarrow{OM}$ = $\overrightarrow{ON}$, với O là một điểm nào đó hoặc $\overrightarrow{MN}$ = $\overrightarrow{0}$

Vấn đề 5. Tập hợp điểm thoả mãn đẳng thức vectơ

Để tìm tập hợp điểm M thoả mãn một đẳng thức vectơ ta biến đổi đẳng thức vectơ đó để đưa về các tập hợp điểm cơ bản đã biết. Chẳng hạn:

Tập hợp các điểm cách đều hai đầu mút của một đoạn thẳng là đường trung trực của đoạn thẳng đó
Tập hợp các điểm cách một điểm cố định một khoảng không đổi đường tròn có tâm là điểm cố định và bán kính là khoảng không đổi

II. Toạ độ

Vấn đề 1. Toạ độ trên trục
Vấn đề 2. Toạ độ trên hệ trục

Chương 2. Tích vô hướng của hai vectơ

Vấn đề 1. Tính tích vô hướng của 2 vectơ
Vấn đề 2. Chứng minh một đẳng thức vectơ có liên quan đến tích vô hướng hay đẳng thức các độ dài

Phương pháp:

Ta sử dụng các phép toán về vectơ và các tính chất của tích vô hướng
Về độ dài ta chú ý AB^2 = $\overrightarrow{AB}$^2
Vấn đề 3. Trong mp Oxy cho tam giác ABC với A(x1; y1), B(x2; y2) và C(x3; y3) xác định hình dạng của tam giác ABC
Vấn đề 4. Trong mp Oxy cho tam giác ABC với A(x1; y1), B(x2; y2) và C(x3; y3) xác định trọng tâm G, trực tâm H và tâm I của đường tròn ngoại tiếp tam giác ABC
Vấn đề 5. Trong mp Oxy cho tam giác ABC với A(x1; y1), B(x2; y2) và C(x3; y3) xác định tâm J của đường tròn nội tiếp tam giác ABC
Vấn đề 6. Trong mp Oxy cho tam giác ABC với A(x1; y1), B(x2; y2) và C(x3; y3) gọi A’ là chân đường vuông góc kẻ từ A lên BC .Tìm A’
Vấn đề 7. Trong mp Oxy cho tam giác ABC với A(x1; y1), B(x2; y2) và C(x3; y3), tính cosA.