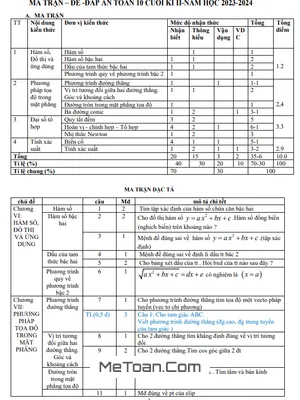
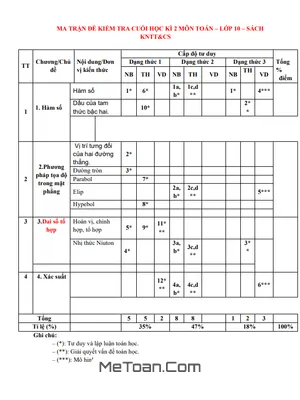
Đề thi HK2 Toán 10 năm học 2019 - 2020 trường Lương Thế Vinh - Hà Nội

Đề thi học kỳ 2 Toán lớp 10 trường Lương Thế Vinh - Năm học 2019-2020
Vào ngày … tháng 06 năm 2020, trường THCS & THPT Lương Thế Vinh, thành phố Hà Nội đã tổ chức kỳ thi kiểm tra chất lượng môn Toán lớp 10 cho học kỳ 2 năm học 2019 – 2020.
Đề thi HK2 Toán 10 năm học 2019 – 2020 của trường Lương Thế Vinh – Hà Nội có mã đề 001, gồm 06 trang với 50 câu trắc nghiệm. Thời gian làm bài thi là 90 phút.
Dưới đây là một số câu hỏi trích dẫn từ đề thi:
Câu hỏi 1: Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: 3x – 4y + 2m = 0 và đường tròn (C): (x – 1)^2 + (y – 2)^2 = 4. Có tất cả bao nhiêu giá trị nguyên của tham số m để trên đường thẳng d tồn tại hai điểm M thỏa mãn từ M kẻ được hai tiếp tuyến MA, MB đến đường tròn (C) (A và B là các tiếp điểm) sao cho tam giác MAB là tam giác đều?
Câu hỏi 2: Tam giác ABC không đều có ba góc thỏa mãn sinA.cosB – cosA.sinB = 0. Khi đó:
- A. Tam giác ABC cân tại B.
- B. Tam giác ABC cân tại C.
- C. Tam giác ABC cân tại A.
- D. Tam giác ABC vuông tại A.
Câu hỏi 3: Trong mặt phẳng tọa độ Oxy, cho ba điểm A(1;2), B(3;-1), C(2;4). Điểm M thuộc đường thẳng x + y + 2 = 0 sao cho biểu thức |6MA – 5MB – 2MC| đạt giá trị nhỏ nhất. Hoành độ x0 của điểm M thỏa mãn?