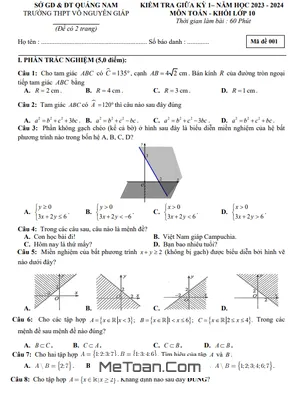
Đề Thi Giữa Kỳ 1 Toán 10 Năm 2025-2026 THPT Nguyễn Thái Bình (Đà Nẵng) Có Đáp Án

Nhằm hỗ trợ quý thầy cô giáo và các em học sinh lớp 10 có một nguồn tài liệu ôn tập chất lượng, chuẩn bị cho kỳ kiểm tra giữa học kỳ 1 sắp tới, MeToan.Com xin chia sẻ bộ đề thi chính thức từ trường THPT Nguyễn Thái Bình, thành phố Đà Nẵng cho năm học 2025 – 2026. Bộ tài liệu này không chỉ bao gồm đề thi mà còn đi kèm đáp án và thang điểm chi tiết, giúp các em tự đánh giá năng lực và củng cố kiến thức một cách hiệu quả.
Đề thi được biên soạn bám sát cấu trúc chương trình sách giáo khoa mới, tập trung vào các kiến thức trọng tâm của nửa đầu học kỳ 1. Đặc biệt, đề thi có sự lồng ghép nhiều bài toán mang tính ứng dụng thực tiễn cao, giúp học sinh phát triển tư duy logic và khả năng vận dụng toán học vào giải quyết các vấn đề trong cuộc sống. Đây là xu hướng ra đề mới giúp môn Toán trở nên gần gũi và thú vị hơn.
Dưới đây là một số câu hỏi tiêu biểu được trích từ đề thi để quý thầy cô và các em tham khảo:
Bài toán tối ưu lợi nhuận: Câu lạc bộ thiện nguyện của trường THPT Nguyễn Thái Bình thực hiện dự án “Trăng Sáng – Lòng Vàng” bán bánh trung thu gây quỹ. Có hai loại bánh là thập cẩm (giá 60 nghìn, lợi nhuận 7 nghìn/cái) và sầu riêng (giá 70 nghìn, lợi nhuận 8 nghìn/cái). Với số vốn không quá 10,5 triệu đồng và tổng số bánh bán ra không vượt quá 160 cái, câu lạc bộ cần bán bao nhiêu bánh mỗi loại để thu được lợi nhuận cao nhất? Đây là một bài toán quy hoạch tuyến tính điển hình.
Bài toán đo đạc thực tế: Để xác định chiều cao CD của tháp chính tại hồ Con Rùa (TP.HCM), người ta tiến hành đo đạc từ hai điểm A, B trên mặt đất (với A, B, C thẳng hàng, C là chân tháp). Biết khoảng cách AB = 17m, góc nhìn từ A đến đỉnh tháp (góc CAD) là 36 độ và từ B (góc CBD) là 49 độ. Yêu cầu tính chiều cao của tháp và làm tròn kết quả đến hàng đơn vị. Bài toán này đòi hỏi vận dụng linh hoạt các hệ thức lượng trong tam giác.
Bài toán về tập hợp: Trong đợt Hội khỏe Phù Đổng, lớp 10/1 có 30 học sinh tham gia. Trong đó, 19 em thi đấu bóng đá và 18 em thi đấu bóng chuyền. Tất cả học sinh đều tham gia ít nhất một trong hai môn này. Nếu gọi số học sinh tham gia cả hai môn là a, hãy tính giá trị của biểu thức 500a. Đây là dạng bài toán sử dụng biểu đồ Ven và các phép toán trên tập hợp.
Toàn bộ đề thi và lời giải chi tiết đã được đội ngũ MeToan.Com biên soạn cẩn thận dưới dạng file PDF, thuận tiện cho việc tải về và in ấn. Hy vọng đây sẽ là tài liệu ôn tập hữu ích, giúp các em học sinh lớp 10 trường THPT Nguyễn Thái Bình nói riêng và trên cả nước nói chung đạt được kết quả cao nhất trong kỳ thi giữa kỳ sắp tới.