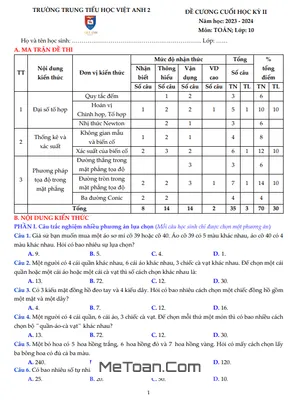
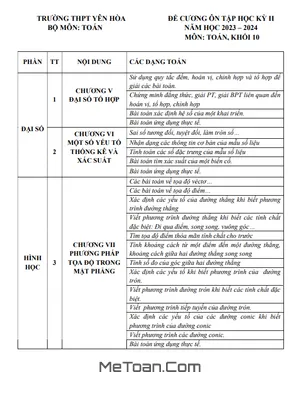
Đề cương ôn tập Toán 10 HK1 năm 2019 - 2020 trường THPT Trần Phú - Hà Nội

Nhằm giúp học sinh khối 10 ôn tập chuẩn bị cho kỳ thi kiểm tra chất lượng học kỳ 1 môn Toán 10 năm học 2019 – 2020, tổ Toán trường THPT Trần Phú, quận Hoàn Kiếm, thành phố Hà Nội biên soạn hệ thống câu hỏi và bài tập trắc nghiệm và tự luận Toán 10 giúp học sinh tự rèn luyện.

Khái quát nội dung đề cương ôn tập Toán 10 HK1 năm 2019 – 2020 trường THPT Trần Phú – Hà Nội:

PHẦN 1: ĐẠI SỐ

A. MỆNH ĐỀ – TẬP HỢP

Học sinh cần nắm được:

• Thế nào là mệnh đề, mệnh đề chứa biến, cách phủ định một mệnh đề, cách lập mệnh đề kéo theo, mệnh đề đảo, mệnh đề tương đương, mệnh đề chứa kí hiệu ∀ và ∃.
• Khái niệm tập hợp và các phép toán trên tập hợp: giao, hợp, hiệu, phần bù.
• Sai số tuyệt đối, độ chính xác của 1 số gần đúng, sai số tương đối, cách viết số quy tròn căn cứ vào độ chính xác cho trước.

B. HÀM SỐ BẬC NHẤT VÀ BẬC HAI

Học sinh cần nắm chắc cách tìm tập xác định của hàm số, biết cách xác định tính chẵn lẻ, tính đồng biến, nghịch biến, biết cách khảo sát vẽ đồ thị hàm số bậc nhất, bậc hai và các phép suy diễn đồ thị hàm số.

C. PHƯƠNG TRÌNH – HỆ PHƯƠNG TRÌNH

Học sinh cần nắm vững:

• Các khái niệm về phương trình, hệ phương trình: tập xác định, điều kiện xác định, các phép biến đổi tương đương, hệ quả, phép giải và biện luận phương trình, hệ phương trình.
• Giải và biện luận phương trình ax + b = 0, ax^2 + bx + c = 0, phương trình chứa ẩn ở mẫu, chứa căn.
• Giải phương trình quy về bậc nhất, bậc hai dạng A = B, |A| = B, |A| = |B|, phương trình tích, phương trình chứa ẩn ở mẫu, phương trình trùng phương, giải các loại phương trình khác, ứng dụng định lí Viét.
• Một số phương trình quy về bậc nhất, bậc hai không chứa tham số.
• Giải hệ hai (ba) phương trình bậc nhất hai (ba) ẩn bằng phương pháp cộng và phương pháp thế.
• Giải và biện luận hệ hai phương trình bậc nhất hai ẩn, giải một số hệ phương trình bậc hai hai ẩn.

D. BẤT ĐẲNG THỨC

Học sinh cần nắm vững các tính chất cơ bản của bất đẳng thức, bất đẳng thức giá trị tuyệt đối, bất đẳng thức tam giác, bất đẳng thức Cosi và hệ quả, bất đẳng thức Bunhiacopxki, các hằng đẳng thức cơ bản để áp dụng vào chứng minh bất đẳng thức.

PHẦN 2: HÌNH HỌC

A. VECTƠ – CÁC PHÉP TOÁN VỀ VECTƠ

Học sinh cần nắm vững các phép toán về véctơ, chứng minh các đẳng thức vectơ, biểu diễn vectơ theo hai vectơ không cùng phương cho trước, chứng minh ba điểm thẳng hàng, dựng điểm, tìm quỹ tích điểm thỏa mãn đẳng thức vectơ, tính tích vô hướng của hai vectơ, chứng minh hai vec tơ vuông góc, thiết lập điều kiện vuông góc.