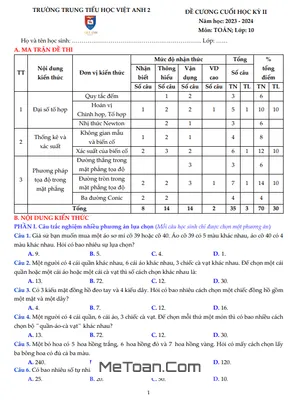
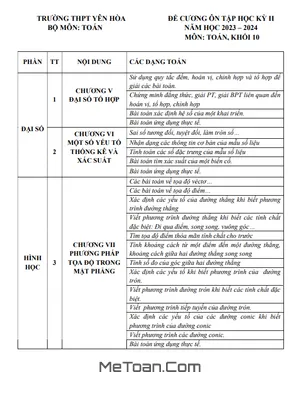
Đề Cương Ôn Tập Học Kỳ 1 Toán 10 Năm 2020 - 2021 Trường THPT Yên Hòa - Hà Nội

Đề Cương Chi Tiết Ôn Thi Học Kỳ 1 Toán 10 - Trường THPT Yên Hòa

Nhằm hỗ trợ các em học sinh khối 10 trường THPT Yên Hòa - Hà Nội trong việc ôn tập và chuẩn bị tốt nhất cho kỳ thi kiểm tra chất lượng giữa HK1 và cuối HK1 môn Toán 10, MeToan.Com cung cấp đến các em đề cương ôn tập chi tiết sau đây:

PHẦN 1. ĐẠI SỐ 10.

CHƯƠNG 1. TẬP HỢP VÀ CÁC PHÉP TOÁN TRÊN TẬP HỢP.

• 1. Trắc nghiệm khách quan:
  • Khái niệm tập hợp, tập hợp con, tập hợp rỗng, tập hợp con thực sự.
  • Các phép toán trên tập hợp: Hợp, giao, hiệu, phần bù.
  • Các bài toán ứng dụng.
• 2. Tự luận:
  • Chứng minh các đẳng thức tập hợp.
  • Giải các bài toán thực tế liên quan đến tập hợp.

CHƯƠNG 2. HÀM SỐ.

• 1. Trắc nghiệm khách quan:
  • Khái niệm hàm số, tập xác định, tập giá trị.
  • Hàm số chẵn, hàm số lẻ, hàm số đồng biến, hàm số nghịch biến.
  • Hàm số bậc nhất, hàm số bậc hai.
  • Các dạng toán liên quan đến đồ thị hàm số.
• 2. Tự luận:
  • Xét tính chẵn lẻ, tính đồng biến, nghịch biến của hàm số.
  • Khảo sát sự biến thiên và vẽ đồ thị hàm số.
  • Giải các bài toán thực tế liên quan đến hàm số.

CHƯƠNG 3. PHƯƠNG TRÌNH – HỆ PHƯƠNG TRÌNH.

• 1. Trắc nghiệm khách quan:
  • Phương trình bậc nhất một ẩn, phương trình bậc hai một ẩn.
  • Hệ hai phương trình bậc nhất hai ẩn.
  • Các phương pháp giải phương trình, hệ phương trình.
• 2. Tự luận:
  • Giải các loại phương trình, hệ phương trình bằng các phương pháp đã học.
  • Biện luận số nghiệm của phương trình, hệ phương trình.
  • Lập phương trình, hệ phương trình từ các bài toán thực tế.

PHẦN 2. HÌNH HỌC 10.

CHƯƠNG 1. VECTƠ.

• Khái niệm vectơ, vectơ cùng phương, vectơ cùng hướng, vectơ đối, vectơ bằng nhau.
• Các phép toán trên vectơ:
  • Tổng của hai vectơ.
  • Hiệu của hai vectơ.
  • Tích của vectơ với một số.
• Trục tọa độ, hệ trục tọa độ, biểu diễn vectơ qua tọa độ.

CHƯƠNG 2. TÍCH VÔ HƯỚNG CỦA HAI VECTƠ VÀ ỨNG DỤNG.

• Giá trị lượng giác của một góc bất kì (từ 0 độ đến 180 độ).
• Tích vô hướng của hai vectơ.
• Ứng dụng tích vô hướng vào việc chứng minh tính vuông góc, tính chất hình học của tam giác, tứ giác.

Lưu ý: Đề cương ôn tập có thể được điều chỉnh cho phù hợp với tình hình thực tế của lớp học.